Question
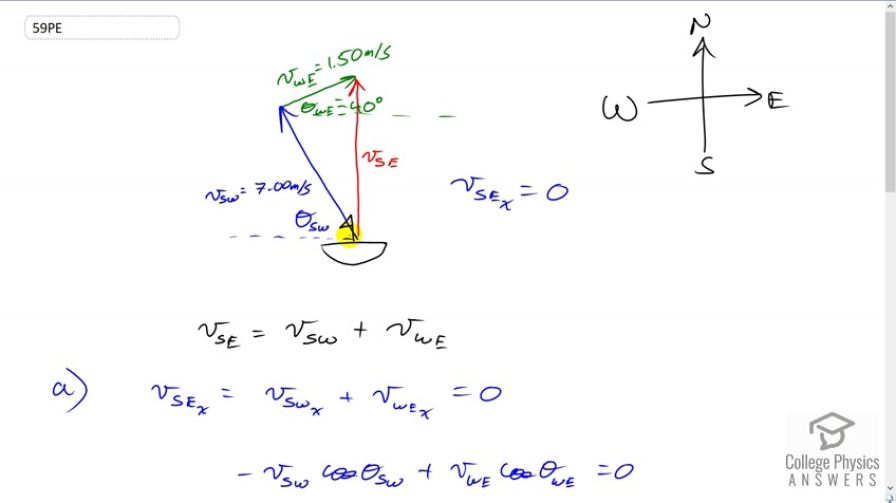
(a) In what direction would the ship in Exercise 3.57 have to travel in order to have a velocity straight north relative to the Earth, assuming its speed relative to the water remains 7.00 m/s? (b) What would its speed be relative to the Earth?
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 3, Problem 59 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
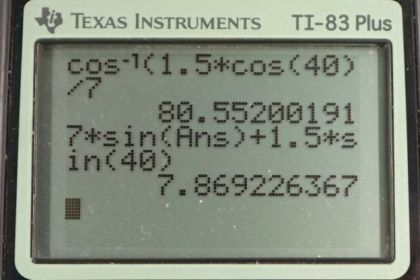
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We know that this ship which is leaving Rotterdam in the Netherlands travels at seven meters per second with respect to the water, and so I’ve labelled its velocity with this blue vector and with subscripts SW. First subscript being the thing that we’re measuring the velocity of and the second subscript being the thing we’re comparing that velocity to. So this is the velocity of the ship, S for ship, with respect to the water W. Now we know that the velocity of the ship with respect to the Earth has to be straight up because the question says figure out what this angle should be such that when combined with the velocity of the water with respect to the Earth, the ship ends up going directly North. So I’ve drawn vectors which add together the velocity of the ship with respect to the water plus the velocity of the water with respect to the Earth because that sum gives us the velocity of the ship with respect to the Earth. You can also see that by looking at the subscripts in this formula where when you add two velocities together, so long as you keep the inner subscripts the same, they’ll end up cancelling and you’ll end up with the velocity of the outer subscripts. So that’s what we have here. The velocity of the ship with respect to the water plus the velocity of the water with respect to the Earth will end up giving us the velocity of the ship with respect to the Earth. So I’ve drawn this blue vector a little bit to the left of North, in order to compensate for the x component of the velocity of the water with respect to the Earth which is to the right. So that they will end up being of equal magnitudes, and so they will add up to zero, resulting in the x component of the velocity of the ship with respect to the Earth being zero, as we’re told it must be. We can write a formula for the x component of the velocity of the ship with respect to the Earth as being the x component of the ship with respect to the water plus the x component of the velocity of the water with respect to the Earth and we’re told that that equals zero, as we wrote up here. That is going to be a negative because it’s pointing to the left of the speed of the ship with respect to the water, multiply by cosine of the angle of the ship with respect to the water, plus, and I write a plus here because this is in the positive direction, the velocity of the water with respect to the Earth multiply by the cosine of the angle of the water with respect to the Earth velocity, using cosine because that’s the adjacent leg of this triangle. All that makes zero and so we can take this term to the right hand side which makes it positive, and then switch the sides around so that the unknown is on the left, then divide both sides by the velocity of the ship with respect to the water. And end up with this line here. Then take the inverse cosine of both sides, and you solve for the angle. It’ll be the inverse cosine of 1.5 meters per second times cos 40 divided by seven meters per second, giving us 80.6 degrees North of West. That’s North of West because it’s towards the North with respect to this line here, which is the negative x-axis or also known as the West axis, you can say I guess. Part b is asking us for what is the velocity of the ship with respect to the Earth in other words, and that’s gonna be, well its y component because it has no x component. So we can find it by adding the y components of the other velocities together. That’s the velocity of the ship with respect to the water times the sine of the angle for the ship with respect to the water velocity and because we’re looking for the opposite leg of this triangle and so we have to use the sine function multiply by the hypotenuse of seven meters per second to get this adjacent, sorry this opposite leg I should say, this being the vSWy there. Then plus the velocity of the water with respect to the Earth times sine of its angle. So that’s seven meters per second times sine of the angle we found before, where I’ve written more digits in here in order to avoid intermediate rounding error, and plus 1.5 meters per second times sin 40, that gives 7.87 meters per second will be the speed of the ship with respect to the Earth.