Question
An arrow is shot from a height of 1.5 m toward a cliff of height . It is shot with a velocity of 30 m/s at an angle of above the horizontal. It lands on the top edge of the cliff 4.0 s later. (a) What is the height of the cliff? (b) What is the maximum height reached by the arrow along its trajectory? (c) What is the arrow's impact speed just before hitting the cliff?
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 34 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
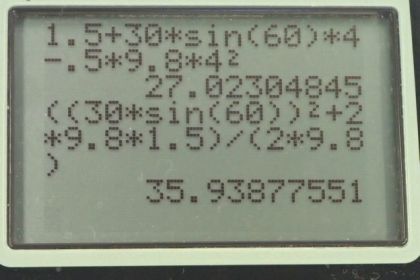
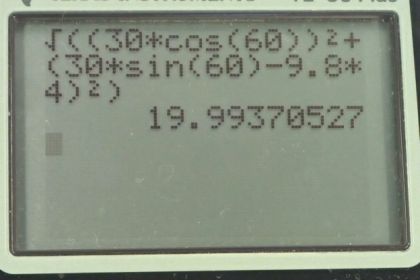
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An arrow is shot at 30 meters per second at an angle of 60 degrees above the horizontal. And it travels for four seconds and then reaches the top of this cliff, which has a height capital h. That we're going to calculate in part A. The arrow begins at a height of 1.5 meters and we'll call that y naught. And part B, we figure out the maximum height that the arrow reaches during its trajectory. And then in part C, we figure out what speed does it impact the top of the cliff with. Okay, so equation 76 in chapter two tells us that, the y-position is the initial y-position plus the initial y-velocity, times time minus one half times acceleration due to gravity, multiplied by time squared. And this is a slightly modified version of that equation where I, you know, make it explicit that we're talking about the y-component of the velocity. And the y-component of this initial velocity will be the velocity v naught multiplied by sine theta. Because this y-component is the opposite leg of this velocity triangle. This is the right triangle. Here is the initial velocity and we have here the components in the x-direction and the components in the y-direction. And this y-component is the opposite leg to this angle theta. And so that's why we use sine, multiply it by the sine theta multiply it by the hypotenuse to figure out this opposite leg. Okay, so we substitute that in here and that's what I show in red down here. And I've also replaced letter y with capital h. Because this is the height that we're trying to find here, it says find capital h, height of the cliff. So the height of the cliff is y naught plus v naught sine theta t. Minus one half g t squared. And now we plug-in all the numbers that we know; So it starts at a height of 1.5 meters, and plus 30 meters per second initial speed, multiplied by sine 60 degrees, times 4.00 seconds, minus one half times 9.80 meters per second squared, times four seconds squared. Giving height of 27 meters for the cliff. And that really deserves only, you know two significant figures probably. Because our initial speed is two significant figures. Okay, then in part B, we figure out the maximum height. So equation 77 says that the final y-velocity, which we know it’ll be zero when the arrow reaches its maximum height. Equals the initial y-velocity squared, minus two times acceleration due to gravity, times the change in height. So the initial y-component of the velocity is v naught sine theta as we talked about in part A. And so we substitute that in, and then we're going to solve this for y. So this minus two g, gets distributed into the bracket by multiplying by each term. And so we have minus two g y plus two g y naught in place of all this. And then we solve for, well, two g y first of all. We have a zero on the left and we add two g y to both sides, and so we have two g y equals v naught sine theta all squared plus two g y naught. Let me divide both sides by two g. And then we get, sorry. We get the maximum height then is v naught sine theta squared plus two g times initial height. Divided by two times acceleration due to gravity. So it’s 30 meters per second, times sine 60 all squared, plus two times 9.8 meters per second squared times 1.5 meters, divided by two times 9.8 meters per second squared. Giving a maximum height of 36 meters. So in this picture this height here is 36 meters, and this height here which we found in part A is 27 meters And lastly we need to figure out the speed with which it impacts the top of the cliff. So the arrow will have some x-component to its final velocity, and some y-component to its final velocity. The x-component is straight forward. Because since there's no acceleration in the x-direction the final x-component of the arrow’s velocity will equal the initial x-component of its velocity. So that’s v naught times cos theta. Cosine, because this is the adjacent leg of this triangle. nd then, we need to figure out an expression for the final y-component of it's velocity; and that's going to be the initial y-component of its velocity, minus acceleration due to gravity, times time. This is equation 75 in chapter two. And we can replace this y-component initial with v naught sine theta. And that’s what we do here, and the final speed then is going to be the square root of the x-component of the final velocity squared, plus the y-component to the final velocity squared. So the x-component is v naught cos theta. That’s what we found here, so we plug that in. And then the y-component is v naught sine theta minus g t. So let me plug-in numbers; So that’s square root of 30 meters per second, times cos 60 all squared, plus 30 minutes per second times sine 60, minus 9.8 meters per second squared, times four seconds all squared. And the square root of that gives us 20 meters per second, is the speed with which the arrow impacts the top of the cliff.
Comments
why is it 9.8 and not -9.8
Hi Coleman, thank you for your question. The factor , strictly speaking, is the magnitude of the acceleration due to gravity. in other words. To indicate the direction downward, which is conventionally taken to be the negative direction, there is a minus in the formula after substituting in place of the acceleration . This can be reviewed in the first few paragraphs at https://openstax.org/books/college-physics-2e/pages/2-7-falling-objects.
All the best,
Shaun
Hello Shaun,
For answer C: Is the reason why the answer isn't -20 because it asked for speed? A scalar quantity? As if it was to ask for the impact velocity as imposed to the speed wouldn't it be negative as the vector is pointing downwards?