Question
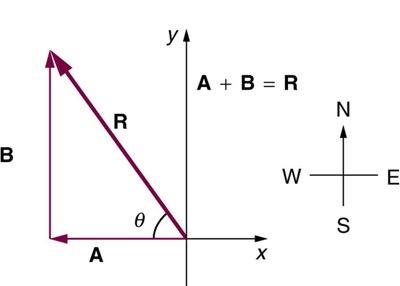
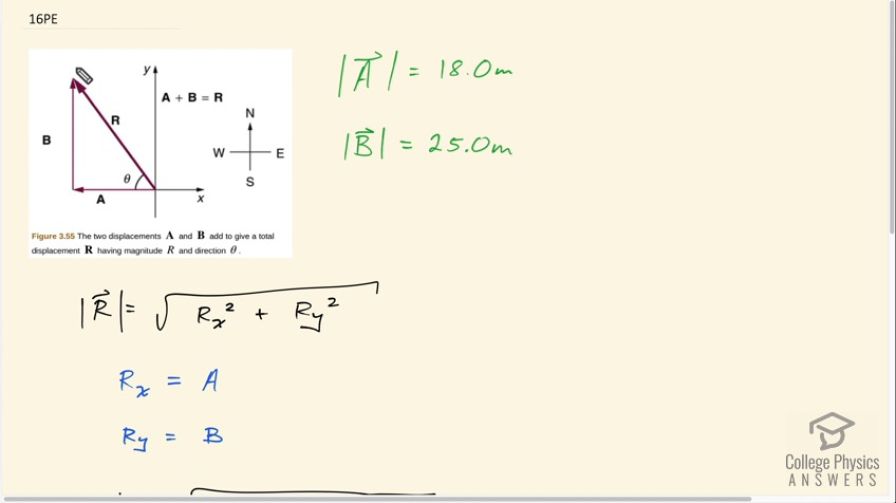
Solve the following problem using analytical techniques: Suppose you walk 18.0 m straight west and then 25.0 m straight north. How far are you from your starting point, and what is the compass direction of a line connecting your starting point to your final position? (If you represent the two legs of the walk as vector displacements and ,as in
Figure 3.58, then this problem asks you to find their sum .)
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 16 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
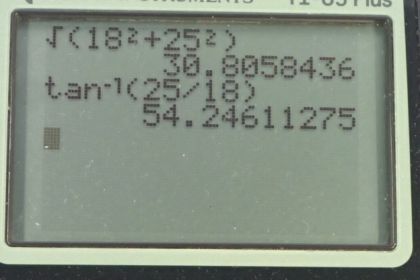
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Imagine that from the starting point, we walk 18 meters to the west and then 25 meters to the north, we would end up here. This line connecting the starting point to the ending point, this arrow, is our displacement vector or the resultant in other words of these two components. We're going to figure out the length of this thing. It's going to be it's x-component squared plus its y-component squared, square rooted. The x-component is going to be the length of the first vector A, which is 18 meters. The y-component will be the length of the second vector B which is 25 meters. The length then of the resultant vector is going to be the square root of 18 squared plus 25 meters squared, giving 30.8 meters. Now the next thing you need to know for a vector is also its direction. We figured out its length so far, we need to figure out this angle theta. Our answer will be such and such degrees north compared to West. This is north of West. We'll take the inverse tangent then of the opposite divided by the adjacent. We can do this because this is a right triangle. The inverse tangent of this y-component of the resultant vector divided by the x-component, the resultant vector in other words. It's the inverse tangent of 25 meters divided by 18 meters, which is 54.2 degrees north of West. Our final answer is that the resultant vector is 30.8 meters long, 54.2 degrees north of West.