Question
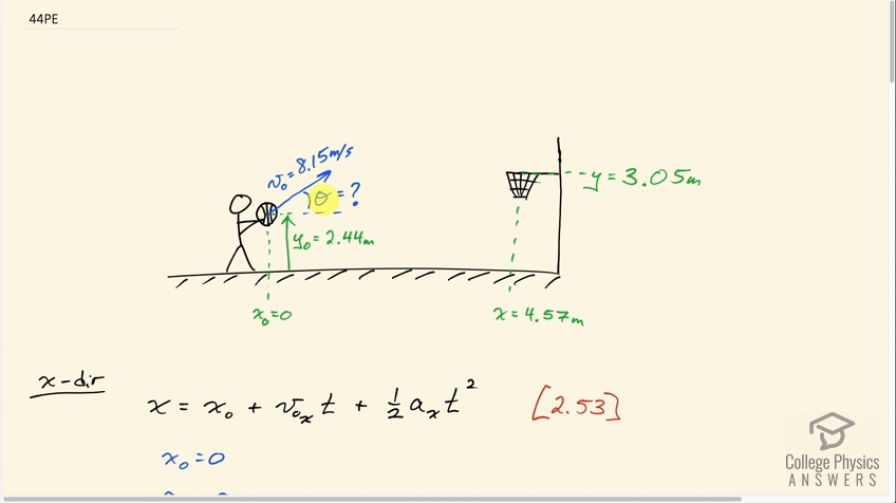
The free throw line in basketball is 4.57 m (15 ft) from the basket, which is 3.05 m (10 ft) above the floor. A player standing on the free throw line throws the ball with an initial speed of 8.15 m/s, releasing it at a height of 2.44 m (8 ft) above the floor. At what angle above the horizontal must the ball be thrown to exactly hit the basket? Note that most players will use a large initial angle rather than a flat shot because it allows for a larger margin of error. Explicitly show how you follow the steps involved in solving projectile motion problems.
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 44 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
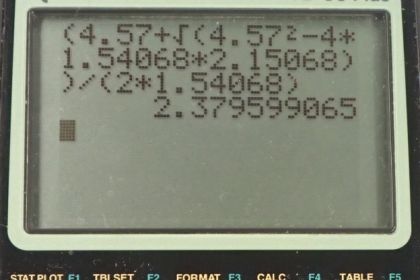
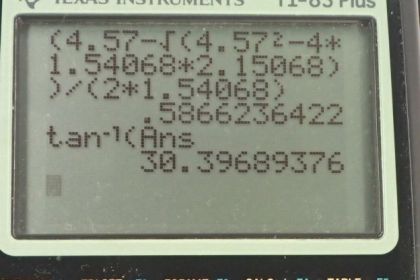
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A basketball player is 4.57 meters horizontally away from the hoop, and the ball is going to begin at a height of 2.44 meters in this player's hands when they're standing up. And the ball will be thrown at the speed of 8.15 meters per second at some unknown angle that we have to figure out. Such that the ball will go into the hoop which is positioned 3.05 meters above the ground. So we've defined x naught to be zero and will take y naught to be 2.44 meters. And then the final vertical position, 3.05 meters. And the final horizontal position, 4.57 meters. So, we're going to figure out this angle. And fasten your seat belt because this question has a lot of algebra involved, and it's a good one to learn some trigonometric identities with. Okay, so let's consider the x-direction to make an equation for that. The horizontal position in the end, will be the initial horizontal position plus the initial x-component of its velocity. Multiplied by the time it takes for the ball to get from here to here. Plus one half times the horizontal acceleration, times time squared. Now of course there is no horizontal acceleration because gravity is pulling only straight down, so a x is zero. The initial position we're defining to be zero. And the initial x-component of the velocity is; the initial speed multiplied by cosine of this unknown angle theta. Because this is the adjacent leg here in this direction for the horizontal component. So if v naught is here, than this would be its horizontal component. And here would be its vertical component. And theta being here makes this the adjacent leg. And so you need cosine of theta multiplied by the hypotenuse to get this adjacent leg. Okay, so that gets substituted in place of v naught x. And that's what I've done here and these other two terms disappeared. So that's equation one. The exposition is the initial speed multiply by cos theta, times time. Now there are two things we don't know in this equation; we don't know theta and we also don't know time. So that means, when you have two unknowns it means you need to have two questions to solve for the unknowns. So the second equation we’ll get by considering the y-direction. And so it’s the same formula but just with the terms for the y-direction; So the final y-position equals the initial y-position plus the initial y-component of its velocity. Multiplied by time, plus one half times the y-component of the acceleration, times time squared. So its acceleration in the y-direction is negative g. And the initial y-component of its velocity is v naught times sine theta. Sine because this is the opposite leg of this right triangle. So we make substitutions there, y naught has to remain y naught, it’s not zero, it's 2.44 meters. So that term remains. And then we have v naught y is being substituted with v naught sine theta. And then the a y is being substituted with negative g. So, we have two unknowns, two equations. We're going to use the method of substitution, which means to change one of the equations to solve for one of the unknowns and then replace that unknown in the other equation. So here's equation one version b; solving for time by dividing both sides by v naught cos theta. And then we have t is x over v naught cos theta. And then we can replace t in this equation two with this. So equation two version b then is y equals y naught, plus v naught sine theta times x. Over v naught cos theta minus one half g x over v naught cos theta squared. So this is the substitution that just happened. That's why this is called the method of substitution for solving a system of equations. So we’ll clean this up a little bit by canceling the v naught’s in this term. And then write this as a single fraction and apply the square to each factor inside the brackets there. And so we have y equals y naught plus x sine theta over cos theta minus g x squared over two v naught squared, cos square theta. So this is an equation and there's only one thing that we don't know which is the theta. But what makes things complicated is that this theta is spread around in among different trig functions in this equation and it's difficult to solve for it. And when that happens, it means we need to think about trigonometric identities. Now sine theta over cos theta is the same as saying tangent theta. That's a trig identity that is useful to put in your memory bank. So, sine theta over cos theta is tan theta. So, we can replace this with tan theta. And now instead of two different trig functions is now a single trig function. Which could be useful, if we could express the second thing also in terms of tan. And we can because this identity is another one that's good to remember; sine squared theta plus cos squared theta equals one. And if we divide each term by cos squared theta, we get sine squared over cos squared plus cos squared over cos squared, which is one, which equals one over cos squared. So divided every single term or both sides, in other words, by cos squared theta. And what happens here, is sine squared over cos squared is the same as tan squared. Because you know, sine over cosine is tangent. And so sine squared over cos squared is the same as sine over cos, all squared. And so given that this bracket is tangent, that means this is tan squared. And so I've switched the sides around to write one over cos squared on the left. And on the right hand side I replace sine squared over cos squared, with tan squared theta plus one. And one over cos squared is exactly what we have here. I mean it's not exactly one over cos squared, it's this g x squared over two v naught squared. But we can think of it as that because this can be written as g x squared over two v naught squared, times one over cos squared. So that's rewriting this term here just to illustrate that we have stuff multiplied by one over cos squared theta. And you can put a negative there if you wanna include that too. Now, this one over cos squared then is getting replaced with tan squared plus one. And so that's what I've done here. And I've also replaced this sine theta over cos theta with tan theta. Then, we can be happy with this because we now have variable in one form squared and in that same form to the power of one. Which means we're going to use the quadratic formula to figure out what this thing is. Now we're going to be figuring out what tangent theta is using the quadratic formula. And then after we know what tangent theta is, we can take the inverse tangent of that answer to get theta. Let's write it out in the usual form for a quadratic equation; with the squared term going first, and the linear term second, and then the constant terms all gathered together last. And, so we have this minus g x squared over two v naught squared distributed in the brackets. So it makes a minus stuff times tan theta and then that same stuff becomes a minus. But I’m also, just for personal preference, I’m multiplying everything by negative one. Because I like to have the squared term have a positive coefficient, that's just what I'm used to doing. So that's what why the signs of everything is going to change. So we have a negative y naught and a negative x tan theta, because getting multiply b this negative one. And then a positive g x squared over two v naught squared, times tan squared theta. and then a positive g x squared over two v naught squared by itself. And then there’s y. Well, we have to subtract y from both sides to put it on the left. Because we want everything to be equal to zero. And then then after subtracting it, it gets multiplied by negative one and so it becomes positive y. Okay, then we need to see that this thing squared. You know tan squared theta is usually written like this. But it could also be written as a tan theta squared like that. This is exactly the same. And I want to write it this way just to really illustrate, that this is the same as the usual you know x squared that you might see there. Although x squared is confusing because it appears over there. But is the thing squared and then the linear term with that thing, the same thing to the power of one. And then a constant term. So, this thing that we're going to solve for is tan theta, and it's going to be negative b plus or minus square root of b squared, minus four a c over two a. And we have to figure out what each of these factors are. So a is g x squared over two v naught squared. So we’ll plug-in numbers; 9.8 meters per second squared times 4.57 meters squared, over two times 8.15 meters per second squared. So this is the horizontal displacement of the basketball, and this is the initial speed. And we get a is 1.54068 meters. So that's the number that we’ll plug-in here. And then b is negative x; And so b is negative 4.57 meters, and then c is all of this stuff here; y minus y naught, plus g x squared over two v naught squared; So it's 3.05 meters final height of the ball, minus the initial height of 2.44 meters. Plus this factor a that we just figured out, 1.54068 meters, which is 2.15068 meters. So now we plug-in numbers to the quadratic formula. So tan theta equals positive 4.57, plus or minus square root of 4.57 squared, minus four times a. And then times c. And then all divided by two a. And we get 2.3716 or 0.586624 depending whether you use the plus or the minus here. So these are two answers, because there are two launch angles that will both make the ball go through the hoop. The small angle, theta ones we’ll call it, is the inverse tangent of this small number which is 30.4 degrees. And then theta two, is inverse tangent of the large answer. Which is 67.2 degrees and is more likely that the basketball player would choose the larger angle. Because then, with that more downward direction as it goes through the hoop. It’ll tend to go through the hoop if their aim is off a little bit. And there we go.
Comments
Hey Shaun just a heads up the text has updated and the initial velocity has been changed to 7.15m/s
Hi johngrose, thank you very much for mentioning this. What version of College Physics are you working from? The online version still lists 8.15 m/s, and I also checked the PDF for the AP version of the College Physics text, as well as a printed version of College Physics.
Look forward to hearing from you,
Shaun