Question
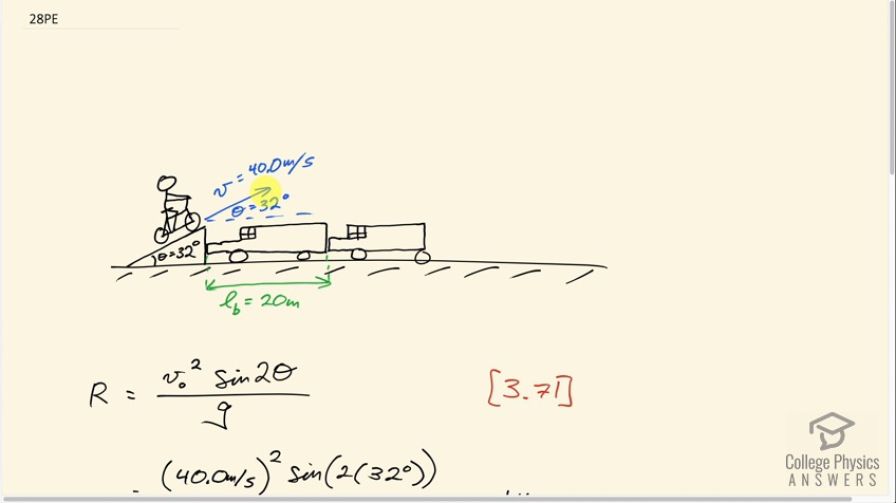
(a) A daredevil is attempting to jump his motorcycle over a line of buses parked end to end by driving up a ramp at a speed of 40.0 m/s (144 km/h) . How many buses can he clear if the top of the takeoff ramp is at the same height as the bus tops and the buses are 20.0 m long? (b) Discuss what your answer implies about the margin of error in this act—that is, consider how much greater the range is than the horizontal distance he must travel to miss the end of the last bus. (Neglect air resistance.)
Final Answer
- 7 buses
- The margin of error is 4.6%. This is not enough, especially considering that air resistance was neglected by our calculation.
Solution video
OpenStax College Physics, Chapter 3, Problem 28 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
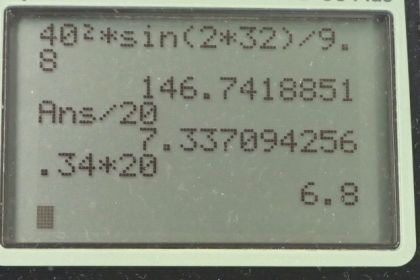
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A motorcyclist launches off this ramp, that's inclined at an angle of 32 degrees with a speed of 40 meters per second. And they're going to hop over a whole bunch of buses and there are more buses that I haven’t drawn here. The question is how many buses can the motorcyclist clear given the speed in this launch angle? So we're told that the roof of the buses is in-line with the top of the ramp. Which means we want to find the range of this motorcyclist, starting from this point. And the range will tell us the distance at the same height of launch where the motorcyclist will return to that height. So this is the range here, from the starting point to the end point assuming the same heights. So we'll figure out what his range is and then will ask how many buses can fit within that range, and that’ll answer part A. So each bus, the length of a bus here is 20 meters and here's a range formula which is given us in chapter three, equation number 71. And this says; the range will be the initial speed squared, multiplied by sine of two times the launch angle, divided by the acceleration of gravity; So that's 40 meters per second squared, times sine of two, times 32 degrees, divided by 9.8 meters per second squared. Giving a range of 146.74 meters. So this range, we can think of as the number of buses, multiplied by the length of a single bus. And we’ll solve for N by dividing both sides by the length of the bus. And so the number of buses that is going to be the range divided by the length of per bus; So it’s 146.74 meters divided by 20 meters per bus. And we can see that units of this fraction work out to buses we could multiply top and bottom by units of bus. And the units of bus would cancel in the bottom, leaving us with, and the meters cancel and leaving us with buses in the top here. So that’s 7.34 buses. If you don't like the way I did that, you could also think of it as 146.74 meters, multiplied by the reciprocal of this denominator. So instead of dividing by a number, you can multiply by it's reciprocal. And the reciprocal of 20 meters per bus is one bus for every 20 meters, and now the meters cancel leaving us with bus. Okay, so we can't have a fraction of a bus and so our answer is going to be seven buses is the number of buses the motorcyclist can clear. Part B asks us, what is the margin of error? And so the error is this extra bit that passed the seventh bus, that the motorcyclist will land. Which is .34 buses and that works out to 6.8 meters because I multiplied this by 20 meters per bus. So buses cancel, leaving us with 6.8 meters. Okay, now this number should be expressed in the context of the total distance traveled here. Because 6.8 meters would be a large margin of error if you're only going five meters. Because it be more than a 100 percent, but in the context of going 146.7 meters this represents only 4.6 percent. So that margin of error is very small considering that we have neglected air resistance. So air resistance is going to make the real distance traveled significantly less than what we've calculated. So I would expect this error is not enough and they should attempt six buses instead of seven.