Question
(a) Repeat the problem two problems prior, but for the second leg you walk 20.0 m in a direction north of east (which is equivalent to subtracting B from A — that is, to finding R' = A - B).
(b) Repeat the problem two problems prior, but now you first walk 20.0 m in a direction south of west and then 12.0 m in a direction east of south (which is equivalent to subtracting A from B — that is, to finding R'' = B - A = - R'). Show that this is the case.
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 3, Problem 7 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
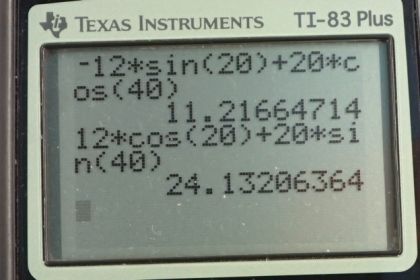
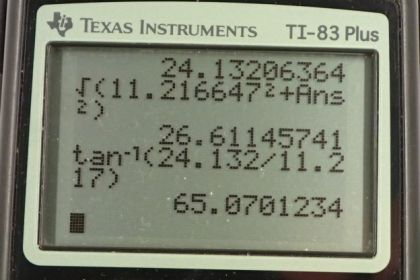
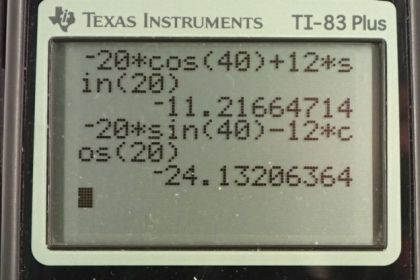
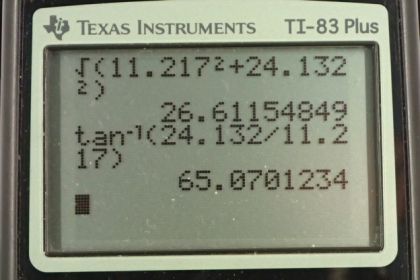
This is College Physics Answers with Shaun Dychko. The route taken in question seven by this person walking is almost the same as the route taken in question five, except the vector B instead of being 40 degrees south of west as it is in question five, it'll now be 40 degrees north of east. So it's in the opposite direction. We'll call it B prime. B prime is the negative of vector B. To find this new resultant which goes from here to there, that's R prime, we'll find the x component will be the sum of the x components of vector A and vector B prime. The y component of the resultant will be the sum of the y components of the vectors that add together. So our x prime is Ax and the vector A, I didn't give it a prime because it is exactly the same as the vector in question five. So to find the x component of vector A, we multiply its length of 12 meters by the sine of 20 degrees because this leg here, that's this bit here, is the opposite leg of this right triangle. So we need to use sine multiplied by the hypotenuse to find the opposite leg. It's in the negative direction so we just put that negative sign there. So it's negative 12 meters times sine 20, then plus the x component of vector B prime. This x component is -- let's get rid of this yellow that's kind of annoying here. This x component of B prime is here, and that is the adjacent leg of this triangle. So we multiply the length of the hypotenuse, 20 meters, by cosine of 40 degrees in order to find the adjacent leg. That's positive because it's directed to the right and this makes 11.217 meters is the xcomponent of the resultant. Then for the y component, we have the y component of vector A is positive because it is directed upwards, and the y component is is here, and it's the adjacent leg of that triangle. So we go 12 times cosine 20 and then plus the y component of B prime is 20 meters times the sine of 40 because this y component is the opposite leg of the triangle. That makes 24.132 meters. So the length of the resultant then, now that we know its components, is the square root of the sum of the squares of the components. So it's the square root of 11.217 meters squared plus 24.132 meters squared giving us 26.61 meters. Then the direction of R prime is going to be the inverse tangent of its y component divided by its x component. So, what we've figured out so far is the x component of R prime and we have figured out the y component of R prime, and what we're finding out now is this angle in here. This is theta prime. We can see that Ry prime is the opposite leg and Rx prime is the adjacent leg of this triangle. So to find this theta we would take the inverse tangent of the opposite divided by the adjacent. So that's inverse tangent of 24.132 meters divided by 11.217 giving us 65.07 and that is an angle towards the north compared to east, so north of east. There we have it. The R prime vector is 26.6 meters, 65.1 degrees north of east. Then in part B, we are told to say that the first leg of the trip is the same as vector B from question five. But then the second leg is the opposite of vector A. So we have initially a route that takes us 40 degrees south of west, 20 meters, and then 20 degrees east of south, 12 meters. So R, we'll call it double prime now, this resultant here, this is R double prime, is vector B plus vector A double prime which I've drawn in green here. The vector A double prime is the opposite of vector A and so this is B minus A. Whereas before we had A minus B, now we have B minus A and our job is to show that well, R prime which is A minus B and which I have re-written here, and we can write this as the negative of bracket B minus A where I just -- you know, I multiplied by negative one twice which is why you can do it because negative one times negative one is one, put a negative in front there and multiply each thing by negative one to change its sign. We end up with negative bracket B minus A. If you were to expand this bracket you would find that the B becomes minus and the A becomes positive and we're left with what we started with. So that's why it's the equivalent. So this is the negative of B minus A which is R double prime. So there we have it. R prime is meant to be the negative of R double prime. It's what we expect in this question is to get our answer of 26.6 meters, 65.1 degrees. Instead of being north of east, we expect it to be south of west. Yep, there. So, let us proceed. Same process as before, the x component of the resultant is going to be the x component of the B vector plus the x component of the A double prime vector. So that's a negative 20 meters because B x component is directed to the left, times cosine of 40 because it's the adjacent leg of this triangle. The x component of the A vector is positive because it's directed in the positive direction, that's this bit here is the x component of the A vector. That's 12 times sine of 20 because it's the opposite leg and so we use sine multiplied by the hypotenuse to get the x component of the A double prime vector. This works out to negative 11.217 meters. For the y component of the resultant, we have B y plus A double prime y, and that's negative 20 times sine 40 because this is the opposite leg of this triangle here and we're going to direct it downward and so put this minus sign there. We have negative 20 times sine 40, and then minus 12 times cos 20. That works out to negative 24.132 meters. Then to get the magnitude of this resultant we take the square root of the sum of the squares. So that's the square root of negative 11.217 meters squared plus negative 24.132 meters squared, giving us 26.612 meters. Then the direction will be the inverse tangent of the y component of the resultant. So just to draw this a little bit out of the way of all the other stuff there, we have a resultant vector here like this and what we've found out so far is its x component and its y component. What we're going to find out now, is this angle here, theta double prime. So it'll be the inverse tangent of the opposite over the adjacent, so the inverse tangent of negative 24.132 divided by negative 11.217, giving 65.07 degrees and that it is towards the south compared to west. So R double prime is 26.6 meters, 65.1 degrees south of west and we were asked to confirm that this R double prime is the opposite of R prime or the negative of R prime in other words, and we have shown that because the magnitude is the same and the angle is of the same size but in the opposite direction, south of west, instead of north of east.