Question
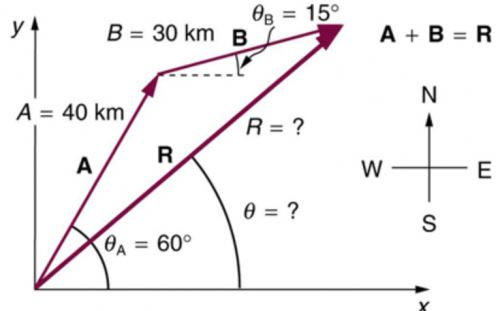
Suppose a pilot flies 40.0 km in a direction north of east and then flies 30.0 km in a direction north of east as shown in Figure 3.61. Find her total distance from the starting point and the direction of the straight-line path to the final position. Discuss qualitatively how this flight would be altered by a wind from the north and how the effect of the wind would depend on both wind speed and the speed of the plane relative to the air mass.
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 24 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
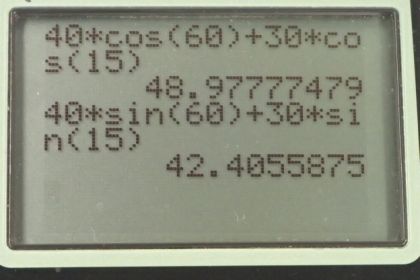
This is College Physics Answers with Shaun Dychko. Flight begins here and travels along path A at an angle of 60 degrees with respect to horizontal, 40 kilometers. And then goes along path B for 30 kilometers at an angle of 15 degrees with respect to horizontal. And the question is what is the resultant of these two legs? What is the straight-line path from the beginning to the end? And so we're adding these vectors together in other words. So, the x-component of this resultant is going to be the sum of the x-components of the vectors A and vector B. And for vector A, the x-component is the adjacent leg of this triangle here. So here is vector A, here’s the y-component upwards and the x-component to the right. And this makes a right triangle here. And we get the adjacent leg by taking the cosine of this angle, and multiply it by the hypotenuse. This is a right triangle. And then vector B, its components will be horizontal, this is Bx. And also vertical, By. And it’s a right triangle and just highlighting that triangle here, there. So is the two triangles we're dealing with. Now, we find the x-component for A by going hypotenuse times cos of this angle. And then for B, we find its x-component by going the length B, multiplied by cosine of theta B. And both of these are positive because they're both directed to the right. So that's 40 kilometers length of A, multiplied by cosine of 60 degrees, plus 30 kilometers which is the length of B, multiplied by cosine of 15 degrees. And this gives 48.9778 kilometers, so that's the x-component for the resultant. And if I were to draw that on here, that's along this dotted line here all the way to the end of the resultant. And then for the y-component of the resultant, that’s going to be the sum of the y-components for vectors A and B. So this component in the y-direction for A is the opposite leg of this triangle. And so we use the sine of theta A, multiplied by the length of A to find it. And then for vector B, likewise sine of theta B multiplied by the hypotenuse. So that's 40 kilometers times sine of 60, plus 30 kilometers times sine 15, which is 42.4056 kilometers. Now to get the length then of the resultant, we have to take the Pythagorean sum of these 2 components; So that it's the square root of the x-component squared, plus the y-component squared. So that’s the square root of 48.9770 kilometers, x-component, squared. Plus 42.4056 kilometers, which is the y-component and we square that. Then we get 64.8 kilometers when you take the square root of that sum. And the direction of this resultant then is the inverse tangent of its y-component divided by its x-component. So its y-component is here. This is resultant y-component and the x-component is, let me put in the right place. It's right here. Okay, and so the triangle we're looking at now, I’ll make it a different color here, I’ll put in blue. This is the resultant triangle. And we want to find this angle theta here, and so we take the inverse tangent of the opposite Ry, divided by the adjacent Rx. That’s what we’ve done here. And so the inverse tangent of 42.4056 kilometers, divided by 48.9778 kilometers, which is 40.9 degrees towards the north, compared to east. So our final answer then is the resultant is 64.8 kilometers, 40.9 degrees north of east. And the question also asked what would happen if there was a wind from the north? Well that would reduce the y-component for both legs of the flight and then therefore reduce the y-component of the resultant. Because the y-component of resultant is the sum of the y-components of these 2 vectors, and they would both be reduced if a wind came from the north. And so that would make this angle smaller, but the x-component would be the same.