Video Transcript
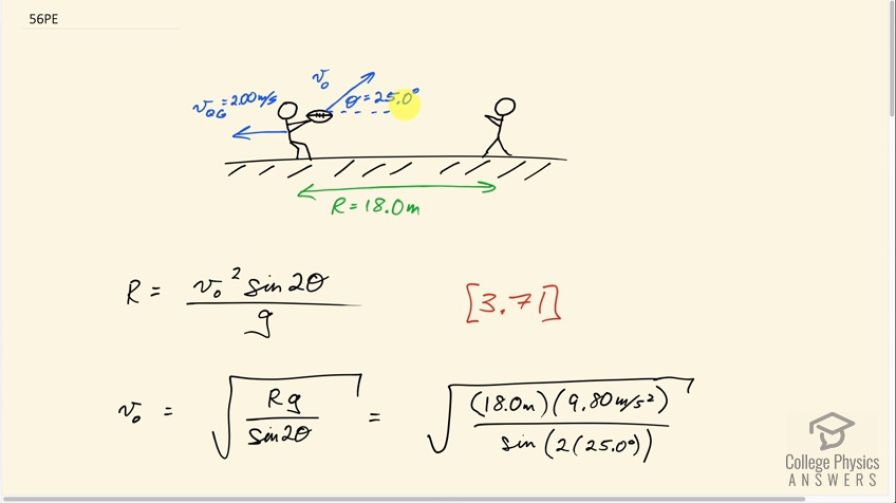
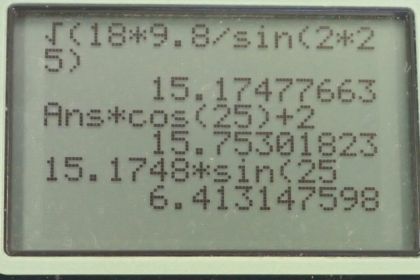
This is College Physics Answers with Shaun Dychko. A football player is throwing a football with some speed that we have to find, at an angle of 25 degrees with respect to horizontal. And this ball is caught by the receiver at the same height, which is convenient because that means we can use this range formula to examine the situation. We're told that the range is 18 meters And the quarterback is moving away from the receiver with a speed of two meters per second. This is equation 71 here, this range formula, and our job is to figure out what is the velocity of the football with respect to the quarterback. This v naught will not be the answer to our question. It'll be the speed of the football with respect to the ground. And then we'll have to do addition of relative velocities to figure out the velocity of the ball with respect to the quarterback. And we’ll get that in the next part of the solution. So the first part of the solution; we’ll figure out this v naught, this speed, and then therefore the velocity of the ball with respect to the ground. And then go from there to figure out the velocity of the ball with respect to the quarterback. So the range of the ball is it's initial speed squared, times sine of two times this launch angle. Divided by acceleration due to gravity and we can solve this for v naught by multiplying both sides by g over sine two theta. And then switching the sides around, and taking the square root of both sides. So the g cancels over here and so does the sine two theta. Then we have v naught squared here, switch the sides around, take the square root of both sides. And we get v naught is the square root of the range, times acceleration due to gravity. Divided by sine of two times the launch angle. So that’s the square root of 18 meters times 9.8 meters per second squared, divided by sine of two times 25 degrees, which is 15.1748 meters per second. I’m keeping lots of digits in this figure because this is an intermediate calculation. And we don't want to do rounding until we get to a final answer. Okay, so this v naught is the, well, you know the speed. But combined with this angle of 25 degrees, it represents the velocity of the ball with respect to the ground. And so I’m using the subscript b for ball, and a subscript g for ground. What the question is asking for is the velocity of the ball with respect to the quarterback. And we're going to use this pattern when adding relative velocities; where if you have two velocities added together, such that their subscripts are the same, these inner subscripts will cancel. Leaving us with the velocity of the outer subscripts. So to get the velocity of the ball with respect to the quarterback, we want the velocity of the ball with respect to the ground. Plus the velocity of the ground with respect to the quarterback. And, now we're not given the velocity of the ground with respect to the quarterback. We're given the velocity of the quarterback with respect to the ground though. And that's two meters per second straight backwards. So if we take the opposite of the velocity that's given to us that of the quarterback with respect to the ground. The opposite of that or the negative in other words, is the velocity of the ground with respect to the quarterback. So by putting a negative sine in front of a velocity, you can switch the order of the subscripts. So we're given this q with respect to g and we want g with respect to q. And so we put a negative inside in front of it to get that. So that’s a negative of whatever this is. And this is negative two meters per second, because we're going to take to the right to be positive. Which means this velocity given to us that of the quarterback with respect to the ground is negative two meters per second. And so we have negative from this pattern of switching subscripts. And then furthermore a negative because that's the velocity of the quarterback with respect to the ground. And in the end that makes positive 2.00 meters per second. The velocity of the ground with respect to the quarterback is two meters per second. So if the quarterback is looking at the ground they would see the ground moving to the right. And so therefore it is positive. So to answer our question, velocity of the ball with respect to the quarterback. We need to take the velocity of the ball with respect to the ground, which we know, 25 degrees. And we figured out it's speed from the range formula. And then add to that using the head to tail method, the velocity of the ground with respect to the quarterback, positive two meters per second. And the resultant then is the velocity of the ball with respect to the quarterback, and this is what we want to find. So, we can find the x-component of this resultant, by adding the x-component of the velocity of the ball with respect to the ground. And this is the adjacent leg of this triangle here. Let's draw it separately over here, let’s put it in green. I’m re-drawing this velocity of the ball with respect to the ground. And has an x-component and a y-component. This is v b g x and this angle here is 25 degrees. And here is v b g y. And this leg here is the adjacent leg, adjacent to this angle, and so we use cosine of that theta. theta being ball with respect to the ground, cosine of that times this velocity of the ball with respect to the ground, and that is the x-component. Okay, and then add to that the velocity of the ground with respect to the quarterback, which is completely in the x-direction. So there's no need to put a subscript on here, because it's all to the right. Okay, and so that’s 15.1748 meters per second times cos of 25 degrees. Plus two meters per second, giving us 15.753 meters per second is the x-component of this velocity of the ball with respect to the quarterback. So this is the x-component of our resultant. Okay, and then we want to find the y-component of our resultant, and the velocity of the ground with respect to the quarterback has no y-components. So that's why I put zero there. And then this y-component is found by taking the sine of this angle times the hypotenuse. And so that's why we have v b g times sine theta b g. So that’s 15.1748 meters per second times sine 25, which is 6.4131 meters per second. So that's the y-component of our velocity of the ball with respect to the quarterback. So then to find the speed of the ball with respect to the quarterback, we take the square root of the sum of the squares of the x & y-components; So that’s the square root of 15.753 meters per second squared plus 6.4131 meters per second squared. Giving us 17.0 meters per second. And then we'll figure out the direction of the velocity of the ball with resp ect to the quarterback, by taking the inverse tangent of it's y-component divided by it’s x-component. So looking at this red triangle here, we have the x-component of the ball with respect to the quarterback found here. And then we have the y-component of the ball with respect to the quarterback, which we found here. And then we wanna find this angle here theta b q. And we take the inverse tangent of the opposite divided by the adjacent. So it’s the inverse tangent 6.4131 divided by 15.753. Which gives 22.2 degrees. So our final answer is 17 meters per second, 22.2 degrees above horizontal. Now, always when you get an answer you should try to do a reality check to see if it makes sense. Does this number make sense? Well, if we look at this picture, we can see that this angle that we're expecting is less than the angle of the ball with respect to the ground. So we expect some answer that's less than 25 degrees, and sure enough it is. So that makes sense. And furthermore, we expect a length of this or a speed in other words to be greater than the speed of the ball with respect to the ground. So we expect a speed that’s greater than 15.17. And sure enough, it is greater than 15.17. So we're feeling confident about this answer and there we go.