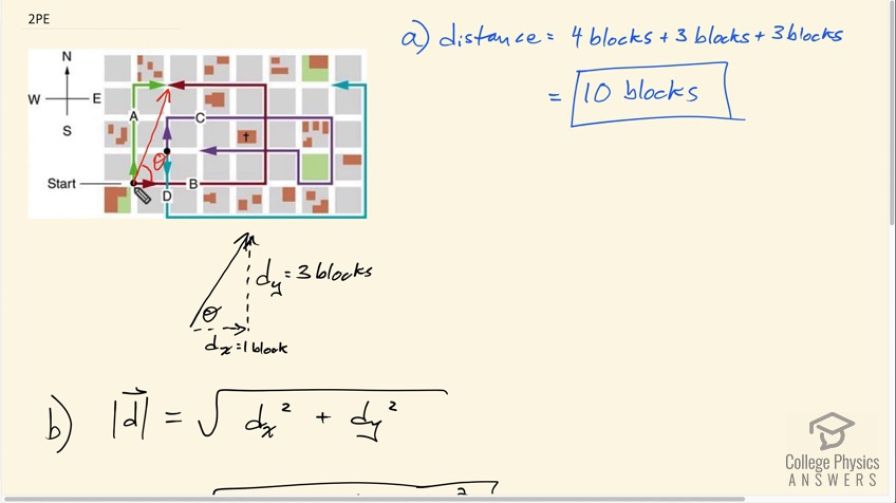
Question
Find the following for path B in Figure 3.52: (a) the total distance traveled, and (b) the magnitude and direction of the displacement from start to finish.

Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 2 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
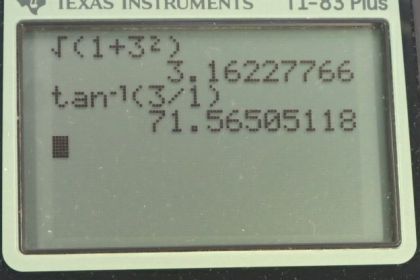
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're concerned with Path B in this question. Here's the start point and along Path B, you travel, one, two, three, four blocks to the east. Then one, two, three blocks north, and then one, two, three blocks to the west. Part A asks us, what is the total distance covered. You add the four blocks here, plus three blocks plus three blocks, that's a total of 10 blocks of distance covered. Then in part B, the question is what is the displacement. The answer to that is going to be very different from our answer to part A. For part B, for displacement, we consider only the start point and the endpoint and the path that we traveled to get to the endpoint does not matter. The only thing that matters is where is that endpoint compared to the start point. A vector, a displacement vector, showing where we started, where we ended would be like this. This vector is going to be the answer to our question in part B. We need to figure out what its components are and it's one block horizontally and then three blocks vertically. I have d subscript y for vertical, three blocks, and then displacement x-component is one block. Then the length of this vector, then this resultant, in other words, is going to be the Pythagorean sum of these two legs of this right triangle. We take the square root of the x-component squared plus the y-component squared. That's the square root of one block x-component squared plus three blocks y-component squared, giving 3.16 blocks as the length of this displacement. Then we also need to specify its direction. That'll be this angle theta which we'll figure out using inverse tangent because we know the opposite leg and we know the adjacent leg. We could also use inverse sine and inverse cosine since we know the hypotenuse now, but it's better to not use some piece of information that we've calculated, better to use information, sort of, not to calculate it. I mean, this isn't really given to us in the question, but at least we want to avoid using numbers that might have errors in them. This is a bit of a complicated arithmetic to get this number and maybe there's a mistake in which case our answer would be wrong if we use sine or inverse cosine. The angle theta is going to be the inverse tangent of the y-component divided by the x-component. It's inverse tangent of three blocks divided by one block, which is 71.57 degrees, and that is towards the north compared to east, so north of east. Our final answer for the displacement vector is 3.16 blocks, 71.6 degrees north of east.
Comments
It's showing that '3.16 blocks' is incorrect. Is there another way of finding the answer? Thanks.
Hi Ashley95, which online homework system are you using? Maybe it's converting from blocks to meters by multiplying by 120 meters per block?
how do you determine the magnitude for path B?