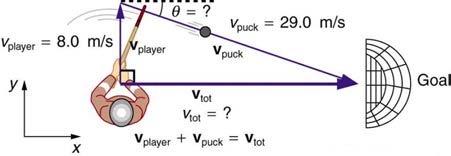
Question
An ice hockey player is moving at 8.00 m/s when he hits the puck toward the goal. The speed of the puck relative to the player is 29.0 m/s. The line between the center of the goal and the player makes a angle relative to his path as shown in Figure 3.63. What angle must the puck's velocity make relative to the player (in his frame of reference) to hit the center of the goal?
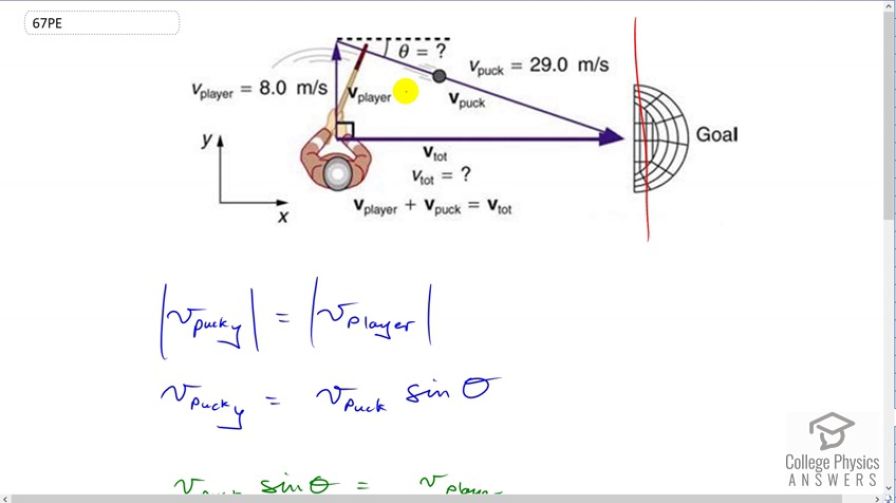
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 67 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This hockey player is moving 8 meters per second parallel to the goal line and he does a slap shot, and the puck moves at a speed of 29 meters per second. It moves its own angle with respect to the horizontal here and the reference frame of the player. So this is the angle that the player would report. Somebody sitting in the stands or in the audience there would perceive the puck as going straight sideways towards the goal. But this hockey player will see the puck as going down at an angle because they're moving forwards. So the question is, what will this angle be? Well, we know the component of this puck's velocity and the reference frame of the player is going to have equal magnitude to the player's speed. So that's what this says here. The velocity of the puck in the y direction is of the same size -- I wrote absolute value signs here just to say ignore negatives. We're just talking about magnitudes here. That's going to be the same as the size of the player's speed or the size of his velocity. So, the y component of the puck's velocity is the velocity of the puck multiplied by the sine of this angle theta because this y component here, this is the y component of the puck's velocity, it is the opposite leg of this right triangle. So we multiply sine theta by this hypotenuse which we're given. So, this equals this, and this equals this, which means these two things equal each other and that's what we say on this line. So v puck times sine theta is equal to the speed of the player. So we'll divide both sides by the speed of the puck and then we get sine theta is that fraction. Then take the inverse sine of both sides and you get theta is the inverse sine of the speed of the player divided by the speed of the puck. So it's the inverse sine of 8 meters per second divided by 29 meters per second which is 16.01 degrees. Now that's not the final answer because the question asked us to find the angle with respect to the player. So that means we have to find this angle in here. Now this full angle here is complementary. These two angles are complementary because they have to add up to make 90 and so we go 90 minus the angle we just found, to give us 74.0 degrees with respect to the player's velocity.