Question
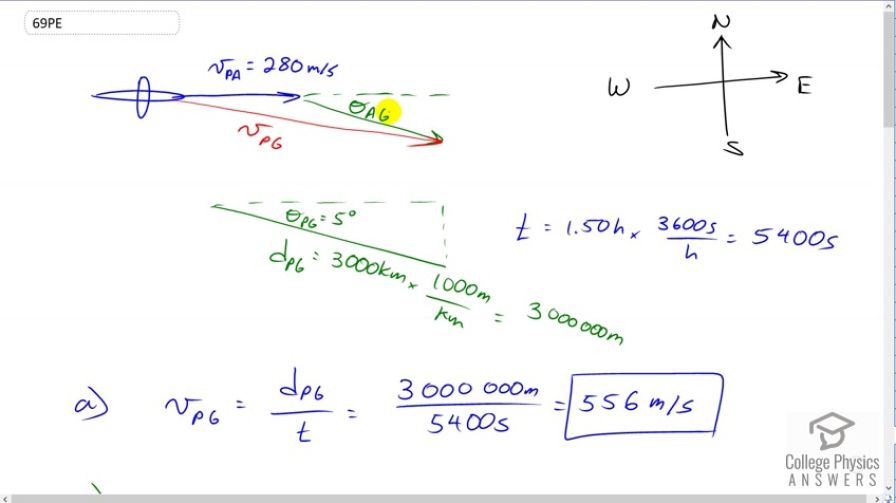
A commercial airplane has an air speed of 280 m/s due east and flies with a strong tailwind. It travels 3000 km in a direction south of east in 1.50 h. (a) What was the velocity of the plane relative to the ground? (b) Calculate the magnitude and direction of the tailwind's velocity. (c) What is unreasonable about both of these velocities? (d) Which premise is unreasonable?
Final Answer
a)
b)
c) & d) see video for discussion.
Solution video
OpenStax College Physics, Chapter 3, Problem 69 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
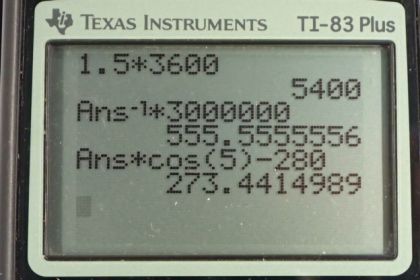
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This plane has an air speed of 280 meters per second and it's going directly east and there's some wind which is going at some angle theta ag, air with respect to the ground, some angle below the east so, to the south of east. It has some speed that we don't really know, and the resultant velocity of the plane with respect to the ground would be this red vector. We're going to figure out what the magnitude of that is in just a second. Now, we're also told the displacement of this plane, that it goes 3000 kilometers in 1.5 hours which is 5400 seconds after you multiply by 3600 seconds per hour. We know that the angle of its displacement is 5 degrees below east because that's the angle of its velocity in the displacement vector will have the same angle as the velocity vector. So, let's figure out the magnitude of this resultant vector. It's going to be the displacement divided by the time. So that's three thousand or three million meters after you convert into meters, and divided by 5400 seconds, gives 556 meters per second. Now, that is one fast plane because the speed of sound is 340 meters per second. So this plane is nearly going at mach two which is suitable for a fighter jet but not for a passenger commercial airline. But anyway, I guess I'm getting ahead of myself, that's part C, we'll talk about that. Okay. The next question is how fast is the wind going such that this is allegedly possible to cover that distance in that time. Well, we know that the resultant velocity of the plane with respect to the ground is equal to the velocity of the plane with respect to the air, plus the velocity of the air with respect to the ground. Notice the inner subscripts are the same and so they cancel leaving us with vpg, the outer subscripts, plane with respect to the ground. We'll solve this for vag. We'll subtract -- we'll subtract vpa from both sides and then switch the sides around. You get vag equals vpg minus vpa. So, the x component of the velocity of the air with respect to the ground is the x component of the velocity of the plane with respect to the ground, minus the x component of the velocity of the plane with respect to the air. Yeah. So, the x component of this resultant here is the adjacent leg of this triangle vpg x adjacent leg of this triangle, and so we'll use the cosine function multiplied by the hypotenuse to find it. Strictly speaking we're using this triangle here but they're the same angle here. This is theta pg in here as well, 5 degrees. This component here vpg x that we're finding. Yeah. Okay. So it's -- and so that's this term here and then subtract away from that vpa because the x component of the velocity of the plane with respect to the air is just that vector because it is entirely in the x direction. So we're taking this red dotted vector minus this blue vector to get the x component of the green vector of the air with respect to the ground. That gives 273.4 meters per second. Now for the y component, we have the y component of the resultant, minus the y component of the plane with respect to the air velocity which is zero because the plane is going directly east with respect to the air. This makes -- it's a minus because it's going downwards. So we're finding this part here to be vpg y. So minus 555.56 meters per second times sine of 5, sine because it's the opposite leg of this triangle. That gives negative 48.42. Now the resultant or the magnitude of the velocity of the air with respect to the ground then is the square root of the sum of the squares of its components. So we take the square root of 273.4 meters per second squared plus negative 48.42 meters per second squared and this gives 278 meters per second. We have an angle, inverse tangent of the y component divided by the x component of the velocity of the air with respect to the ground. That gives 10 degrees and that is south of east as we can tell from this picture here. So, we just found this theta ag is 10 degrees towards the south compared to east. So that's the final velocity for the air with respect to the ground. Now that's very fast. It's almost the speed of sound. I think it's unlikely that wind can actually blow that fast. So we can say that that's unreasonable as well as the speed of the plane is also unreasonable because only -- well, I guess the Concorde goes faster than mach one but it's not even flying anymore. I can't think of any passenger jets otherwise that can go faster than the speed of sound. They're very noisy when they do that and so people would complain about them flying overhead and it also takes a lot of fuel to break the sound barrier because the sound barrier is a physical thing. It's a buildup of high pressure air in front of the plane and it's difficult to penetrate that. So it's not economical to fly faster than the speed of sound. So part D, the unreasonable premise here is to say that the plane traveled 3000 kilometers in one and a half hours. Saying that the plane goes at an air speed of 280 meters per second is fine but either this distance is too much or this time is too little. And there we go!