Video Transcript
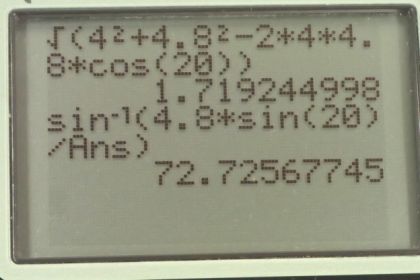
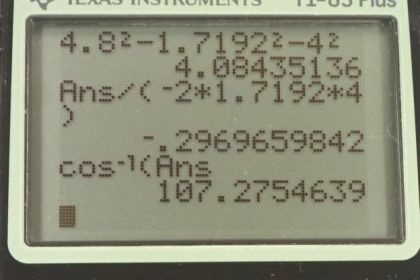
This is College Physics Answers with Shaun Dychko. This question tells us what the velocity of the ship is with respect to the water and it's 4 meters per second, 25 degrees west of north. So that would be a line that is like this, where this is 25 degrees in here. And that's what we learn from when we look at the question text here, and it says 25 degrees west of north. And then the Gulf Stream is another word for the water. It's a certain current that flows in the Gulf of Mexico. And it's traveling 4.8 meters per second, five degrees west of north. And so we write that piece of information down as well; 4.8 meters per second, five degrees west of north. I've been careful about how I've chosen subscripts here, this is very important to choose good subscripts. As you'll see in this line here, when we figure out how to get the answer for what is the velocity of the water with respect to the Earth. So the subscripts have two letters; The first letter is the thing that's moving, in this case it's the ship. And the second letter says what the velocity is compared to. So this is with respect to the water or compared to the water. So the velocity of the ship compared to the water is denoted v s w. And the velocity of the ship with respect to the Earth is v s e, e standing for Earth. Okay, and the question asks us, what is the velocity of the Gulf Stream? And it doesn't say what to compare the velocity to, and so we have to make an assumption that it must be compared to the Earth. And so that's why we have v w e, the w standing for water or Gulf Stream compared to the earth. Now when you're adding relative velocities, you set it up so that the inner subscripts are the same and then the outer subscripts are the things that you want. So we want to have velocity of the water with respect to the Earth. So that means we need to add the velocity of the water with respect to the ship, plus the velocity of the ship with respect to the Earth. When you have the inner subscripts the same, they will cancel. Leaving you with the velocity of this first letter with respect to this last letter. So we're not given the velocity of the water with respect to the ship. But we are given the velocity of the ship with respect to the water. And then what we want is going to be the opposite of what we're given. And so we just put a negative sign in front of it. Which is to say that we draw a vector going in the exact opposite direction. So we have 25 degrees west of north given to us, and it's opposite is gonna be 25 degrees east of south. The opposite of west is east and the opposite of north is south. And so whereas this vector here is what we’re given initially. This is v s w and this angle here is 25 degrees. The opposite will be this line here. This is v w s. And then this angle is 25 degrees. These are opposite angles. So there we go. That's what this vector is; velocity of the water with respect to the ship. And that's what we want in order to answer our question. So we add this vector, plus this vector to get our final answer. And so we draw those two vectors on here. Here’s the velocity of the water with respect to the ship. That's what I drew here. And it has a length of four meters per second. And, sorry, four meters per seconds. And then add to that the velocity of the ship with respect to the Earth, which is given to us, 4.8 meters per second, five degrees west of north. So this dotted white line here represents north, and we're going to go five degrees to the west of that. And that's this green vector is the velocity of the ship with respect to the Earth. Okay, and then the resultant will be from the tail of the initial vector to the head of the final vector. And this will be the velocity of the water with respect to the Earth. And that's going to be our answer, we have to figure out what that vector is. So we can figure out it's length using the cosine law, because we know the length of this side, and we know the length of this side. And we can figure out what this enclosing angle theta is. Now these two dotted white lines are parallel, and so this blue line is a transversal between them. And so that means this angle 25 which we're given, is opposite to this angle in here between the dotted line and the blue. So this whole angle here is 25, but theta is not 25. theta is going to be this 25 minus this angle here, which is five. And so theta is going to be 20 degrees. And now that we know this enclosing angle between these two known side lengths, we can figure out what the length of the opposite side is using the cosine law. And that's written here where if you have three sides and you label them each with little letters a, b and c. And you have the angles opposite to each side will be their capital letter counterpart. So this is capital B because it's opposite some side little b, this is a capital A because it's opposite side little a. And capital C is opposite side little c. So little c is like v w e that we want to find and c squared is a squared plus b squared, minus two times the length of a, times the length of b, times cosine of this angle between these two known sides. So, we take the square root of both sides to figure out the length of little c or the length of velocity of the water with respect to the Earth in other words. And so it’s gonna be the square root of the velocity of the water with respect to the ship squared, plus the velocity of the ship with respect to the earth squared, minus two times the product of those velocities, times cosine of the angle between them. So we have the square root of four squared plus 4.8 meters per second squared, minus two times four times 4.8 times cos 20, and that gives 1.7192 meters per second. This is not our final answer, we're going to round that to three significant figures. But for now, we’ll keep all those digits. Because they're going to use this number in a subsequent calculation for figuring out the direction of the water with respect to the Earth. So to figure out the direction of this vector, we'll use cosine law again and we'll use it to figure out this angle alpha between the red and the blue. And then once we figure that out, we'll take these straight line angle 180. Take away the alpha that we find, take away 25 as well and we'll be left with this portion up here, which we'll call beta. Which will be the direction of this vector. And that'll be some number of degrees east of north. So, here’s cosine law again. Where we’ve called the opposite side v s e. And so that side squared equals v w e squared plus v w s squared, minus two times v w e times v w s. Times cosine of this angle alpha, and we know all the side lengths. And, so we can rearrange this to solve for alpha. So we take these two terms, subtract them from both sides or in other words move them to the left side. And then also divide by these factors; Negative two v w e v w s on both sides. And then take the inverse cosine of both sides. So that's a whole bunch of things done at once. I hope that's easy enough to follow. And then you solve for alpha that way. So alpha is going to be the inverse cosine of 4.8 meters per second squared, that's v s e. Minus v w e which is four meters per second squared, minus the velocity of the water with respect to the Earth that we calculated before and square that. Divided by two times four times 1.7192. And you take the inverse cosine of all that and get 107.28 degrees. So this angle in here is 107.28. And then that is taken away from 180. And also 25 is taken away as well from 180. And you end up with 47.72 degrees, and that is towards the east compared to north. So our final answer, velocity of the Gulf Stream or the water with respect to the Earth is 1.72 meters per second, 47.7 degrees east of north.