Question
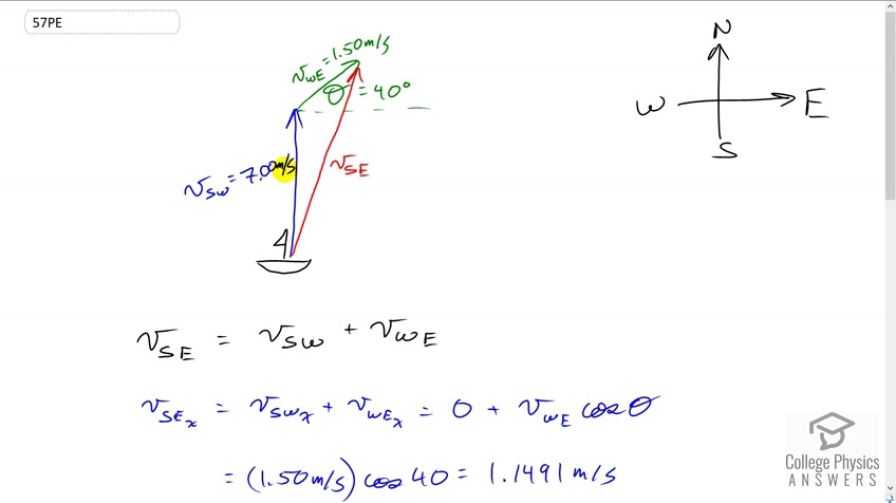
A ship sets sail from Rotterdam, The Netherlands, heading due north at 7.00 m/s relative to the water. The local ocean current is 1.50 m/s in a direction north of east. What is the velocity of the ship relative to the Earth?
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 57 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
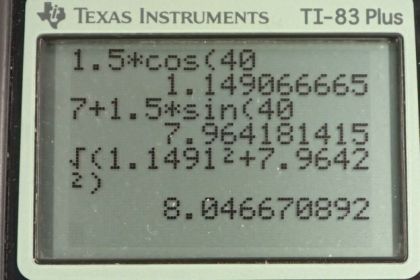
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This ship leaving Rotterdam in the Netherlands is going due North at 7.0 meters per second, and that’s with respect to the water. And so that’s how I’ve written the subscripts here. S is the first subscript for the thing that’s moving and W is the subscript for the thing the movement is compared to. So this is the velocity of the ship with respect to the water. Add to that the velocity of the water with respect to the Earth, going at 40 degrees North of East at a speed of 1.5 meters per second and you get the velocity of the ship with respect to the Earth when you add them together. We can tell that first of all based on this vector picture, we can also tell that based on the subscripts. When you add two relative velocities together, if you keep the inner subscripts the same, then they will cancel. So this and this are the, these are the inner subscripts and so velocity of the ship with respect to the water plus the velocity of the water with respect to the Earth, add those together, the inner subscripts always cancel and you’re left with the velocity of the ship with respect to the Earth. We’re left with the velocity consisting of the outer subscripts. The x component of the velocity of the ship with respect to the Earth will be the x component of the two vectors that are being added together. This first vector here has no x component, so zero. We add to that the velocity of the water with respect to the Earth multiplied by cos theta because this is the adjacent leg of this right triangle here. That’s 1.5 meters per second times cos 40 which is 1.1491 meters per second. Then to get the y component of the velocity of the ship with respect to the Earth, we add the y components of each of the other vectors together. The velocity of the ship with respect to the water is entirely in the y direction so we can just write down seven meters per second, no need for trigonometry there. Then as for the velocity of the water with respect to the Earth, we’re looking for the opposite leg of this triangle so we use the sine function, multiplied by the hypotenuse to get it. So that’s 1.5 meters per second times sin 40 giving us 7.9642 meters per second is the y component of the velocity of the ship with respect to the Earth. Then, to get the length of the velocity of the ship with respect to the Earth, we take the square root of the sum of the squares of each of its components, so it’s the square root of 1.1491 meters per second squared plus 7.9642 meters per second squared, that gives 8.05 meters per second. It’s direction, we’ll take the inverse tangent of its y component divided by its x component, and so since we’ve set it up that way, the angle that we’re finding is this one, with respect to horizontal, with respect to the East, so we’re going this number of degrees North of East. I put a subscript SE on this theta to say that it’s the angle of the ship with respect to the Earth. Then we’re taking the inverse tangent of the opposite divided by the adjacent of this triangle here. So that’s the inverse tangent of a, I guess I should write down the numbers there shouldn’t I. Let’s do that. It’s the inverse tangent of the y component which is 7.9642 divided by the x component of 1.1491, that gives 81.8 degrees, which is North of East. So our final answer for the velocity of the ship with respect to the Earth is 8.05 meters per second, 81.8 degrees North of East.