Question
A basketball player is running at 5.00 m/s directly toward the basket when he jumps into the air to dunk the ball. He maintains his horizontal velocity. (a) What vertical velocity does he need to rise 0.750 m above the floor? (b) How far from the basket (measured in the horizontal direction) must he start his jump to reach his maximum height at the same time as he reaches the basket?
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 46 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
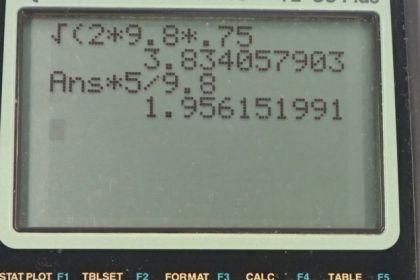
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A basketball player is running horizontally at five meters per second. And they're going to jump and they’re going to have some initial vertical component to their velocity in other words, that we have to find. Such that after they jump, they will reach a height of .75 meters when they're at the position of the basket. So, in part A, we first have to ask what vertical component to the velocity do they need in order to get .75 meters up into the air? So equation 77 in chapter two says that, the final vertical velocity squared, equals the initial vertical component of the velocity squared, minus two times acceleration due to gravity, times the change in their vertical position. We’ll take y naught to be zero, and the final y-velocity is also going to be zero when they get to their maximum height. And so we can substitute zero for v y and zero for y naught. And then we have this minus two g y term here, which we add to both sides to get to the other side. And then switch sides around, so have v naught y squared equals two g y. Then we take the square root of both sides and v naught y is plus or minus the square root of two g y. So it's plus or minus a square root of two times 9.8 meters per second squared times .75 meters. And we know from our picture that they're going to be going upwards. Which is the positive direction we’ll say, in which case we'll take the positive square root here. So we have the initial y-component to their velocity is 3.83 meters per second. Then in part B, so x is going to be the position of the basket, such that when they start at x naught equals zero. And they jump with this speed that we found in part A, and they raise his height .75 meters, they’ll be at .75 meters when they're at the basket. Okay, so x naught is zero because we define the initial position to be that way. v naught x is just v x because there's no acceleration horizontally as we say here. And so there's no need to distinguish between initial or final x-component to velocity, it’s just constant all the time. It’s going to be five meters per second. And then after those substitutions, we end up with the position of the basket then is going to be the v x times time. Now we don't know what time is but we can figure it out using the y-direction. We know that the final y-velocity, which will be zero when they get to the top of their jump, is going to equal the initial y-component to their velocity which we found in part A minus g times t. And we can add g t to both sides. And this term is zero. And then divide both sides by g to solve for t. So t is v naught y over g. So we plug that in to this equation for x. Which we've done here, and so the basket will have the position 1.96 meters. Or in other words the player has to be 1.96 meters horizontally away from the basket. And we found that by going five meters per second horizontal velocity, times 3.83406 meters per second vertical component to their initial velocity, divided by 9.8 meter per seconds squared. There we go.
Comments
hi Shaun, when is g positive 9.8 vs -9.8? Wouldn't it always be negative, since it's acting against the y at all times?
Hello Kate, is meant to always be the magnitude of the acceleration due to gravity. Having down be the negative direction is itself a convention, albeit a very common one. Nevertheless, when someone takes down to be the positive direction, the acceleration due to gravity would be , or . In short, is always positive, and a negative sign is placed in front when the chosen coordinate system says that down is the negative direction.
Hope that helps,
Shaun