Question
A football player punts the ball at a angle. Without an effect from the wind, the ball would travel 60.0 m horizontally. (a) What is the initial speed of the ball? (b) When the ball is near its maximum height it experiences a brief gust of wind that reduces its horizontal velocity by 1.50 m/s. What distance does the ball travel horizontally?
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 3, Problem 47 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
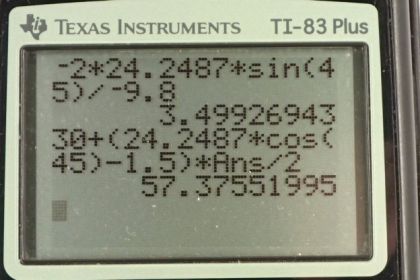
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. When this football is punted at an angle of 45 degrees, it has a range of 60 meters. And so we can use the range formula, since the final level of the ball will be the same as the initial level and we can use this to find the initial speed. We’ll solve this for v naught by multiplying both sides by g over sin two theta. And then switch the sides around and take the square root of both sides, giving us v naught is the square root of the range times acceleration due to gravity divided by sine of two times the angle. So it’s the square root of 60 times 9.8 and that gives 24.2 meters per second, is the initial speed. Then in part b, we’re told that the ball as its travelling along its trajectory will experience a gust of wind at halfway point that reduces its horizontal velocity by 1.5 meters per second. There’s gonna be two intervals to consider here. The first interval is before the gust of wind happens, between the initial x and x1. And the second interval of time will be from here to x2. Now the time intervals will be the same because this gust of wind occurs at the halfway point. So this occurs at t1 which is the total time divided by two. We know what the position is here, because since it’s the halfway point, it’s half of 60. So x1 is 30 meters. Now the part where we need to do some work though, is to figure out what is this x2. We know what the time interval t2 is, it’s also gonna be the total time over two. We’re going to calculate the speed during the second interval, and it’s gonna be the initial x component of velocity minus 1.5. When we plug this speed and this time into our horizontal position formula, we will find its final position x2. It’s gonna be x1 plus the speed during the second interval multiply by the time of the second interval. So we need to know what the total time in the air is though. To do that, we consider the vertical direction and so the final y position equals initial y position plus the initial vertical component of its velocity times time plus one half times the vertical acceleration times time squared. The final initial heights are both zero so that makes it a bit more convenient. We’re solving for t by the way so we are subtracting v naught y and t, that factor, that term I should say, from both sides and then we’re left with this line but I’ve substituted v naught times sin theta in place of v naught y because that’s the vertical component of this velocity. And it’s the opposite leg of this triangle. To find the opposite leg, you take the sine of the angle multiply by the length of the hypotenuse. And then we divide both sides by t and also divide both sides by ay and multiply both sides by two. Let’s write that a bit nicer here. And then multiply this by two over ay t and so the t is cancel on the right, and you’re left with t to the power of one on the left. And of course the two and the ay cancel on the left, isolating t. On the right hand side, we’re left with negative two times initial speed times sin theta over vertical acceleration. So that’s negative two times 24.2487 meters per second that we calculated in part a, times sin 45 divided by negative 9.8 meters per second squared, giving a total time of 3.4993 seconds in the air. This gust of wind since it affects only the horizontal direction, has no effect on the amount of time that the ball spends in the air. It still spends the same total time in the air. We move on to this part of our work. Now we know what t2 is, being half of the total time. We have now calculated the total time so we can figure out what t2 is and v2 is the horizontal component of the initial velocity minus the 1.5 meters per second resulting from the gust of wind. We’ll substitute this and this into here, to get this line here. So x2 is x1 plus v naught cos theta minus one and a half, all times t over two. So plugging in numbers, 30 meters plus 24.2487 meters per second times cos 45 minus 1.5, all times the total time of 3.4993 seconds over two, gives a final range of 57.4 meters. As a result of this gust of wind, our range is now less than 60, and so this answer makes sense.
Comments
can you also say that ymax is reached at 30m, as this is half of 60m. as vix = 17.1m/s (cos45deg*24.2), t for part A is simply 30/17.1 = 1.75s. Then, as we know Part B also lasts 1.75s and the new horizontal speed is 17.2-1.5 = 15.6m/s, in part B distance travelled = 27.4m. Overall range is then 57.4m.