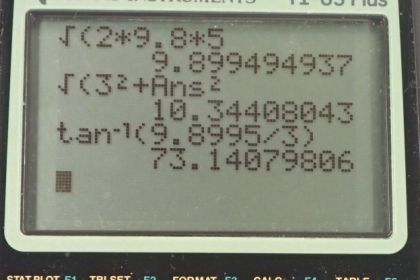
Question
An eagle is flying horizontally at a speed of 3.00 m/s when the fish in her talons wiggles loose and falls into the lake 5.00 m below. Calculate the velocity of the fish relative to the water when it hits the water.
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 40 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This eagle has a fish in its talons at a height of five meters. And the eagle is moving to the side with a speed of three meters per second. And then the fish wiggles and gets free of the talons and starts to fall. And the question is what velocity will the fish have when it hits the water? And that velocity will have two components; one will be its x-component and that isn't going to change as it falls. The x-component of its velocity will continue being 3.00 meters per second during the fall. Because there's no acceleration horizontally, we’re ignoring air friction. The y-component of its velocity though will be increasing as it falls. Because it's accelerating due to gravity. And when it finally reaches the water, that’ll have a velocity that'll have these two components. And we’ll have to have those components together using the Pythagorean theorem to figure out the resultant final speed. And then we’ll also figure out the direction by taking the inverse tangent of the y-component of the velocity, divided by the x-component of the velocity, to figure out this angle theta, this angle below horizontal. So after we find its speed and its direction, then that is the velocity of the fish. So the final x-component of its velocity will be the initial x-component of its velocity. Which is three meters per second. And we’ll use equation 77 from chapter two to figure out the y-component of its velocity when it hits the water. So its final velocity squared will be its initial velocity squared, minus two times acceleration due to gravity. Multiplied by the change in position. So that’s the final position minus the initial position. So the initial position is five meters above the water. The final position is zero. Because we're going to take the water to be our reference level, and we’ll just assign it a position of zero. And its initial y-component of its velocity is zero. Because it isn't falling when it's in the talons of the fish or of the eagle. Okay, so that is to say that this term is zero and this term here is also zero. And so we distribute this two g into the brackets, but we're just multiplying negative two g by negative y naught which gives us positive two g y naught. Let me take the square root of both sides, and when doing that, we can take the positive or the negative square root of the right hand side. And we'll choose one of these depending on our understanding of the situation. And we're going to choose negative. Because we're taking down to be the negative direction. Okay, usually I guess we say, we specify what direction is positive. So I guess upwards is positive and to the right is positive. Okay, so that is the square root of two times 9.80 meters per second squared, times its initial position of five meters. And that is negative 9.8995 meters per second. So then we plug into this formula for the final speed; this v final x-component squared, plus v final y-component squared, all square rooted. So that's three meters per second squared, plus negative 9.8995 meters per second squared. And this square root of all that gives us 10.3 meters per second. Then the direction will be the inverse tangent of the opposite leg here. This is the opposite leg of this right triangle to the angle theta, and divide that by the adjacent leg. Then take the inverse tangent of that quotient, then we'll get the angle. So it’s the inverse tangent of 9.8995 meters per second, divided by three meters per second. Which is 73.1 degrees and that is below the horizontal. So our final velocity then, speed and direction is 10.3 meters per second, 73.1 degrees below horizontal.
Comments
why isn't g -9.8m/s^2? isn't it going down in the y direction?
That's a good question. You're quite right that, with the convention coordinate system of up positive, the acceleration is . However, , is the magnitude of the acceleration due to gravity. It's always positive. Equation 2.77 already accounts for direction by putting a minus in the formula. In its original form the formula is , which is adapted for the vertical direction with positive up into by replacing with .
Hope this helps,
Shaun