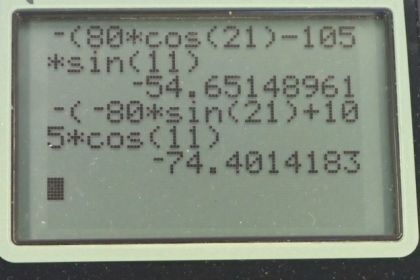
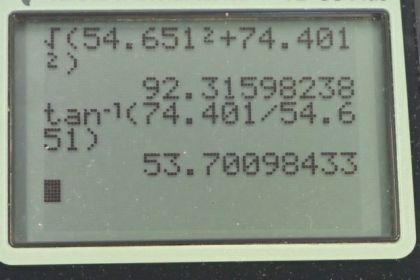
Question
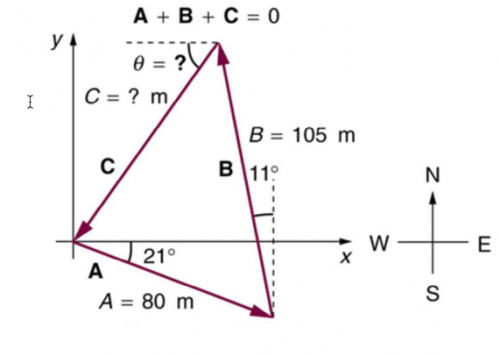
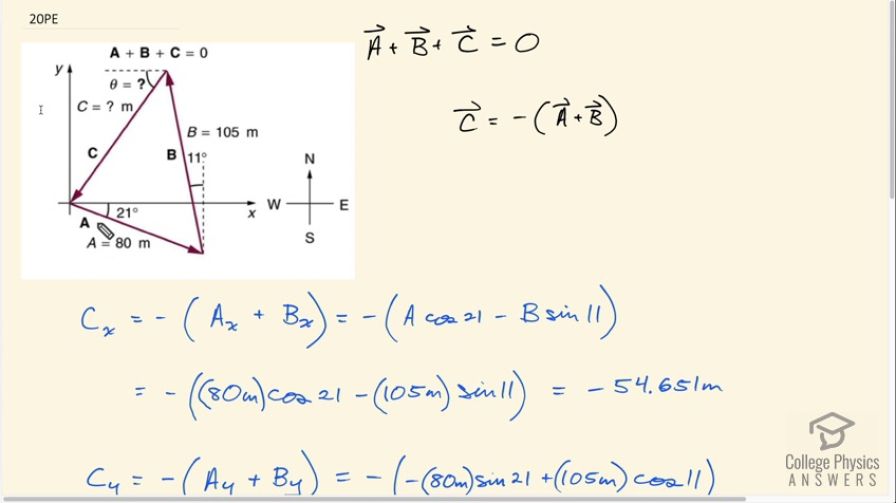
A new landowner has a triangular piece of flat land she wishes to fence. Starting at the west corner, she measures the first side to be 80.0 m long and the next to be 105 m. These sides are represented as displacement vectors A
from B in Figure 3.59. She then correctly calculates the length and orientation of the third side C . What is her result?
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 20 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In putting fencing around this triangular garden, we have Vector A given to us of length 80 meters, 21 degrees to the south of East, and then vector B, which is 105 meters, 11 degrees to the west compared to north. Then we have to figure out what is this final Vector C that finishes the enclosure. We know that the vectors A, B, and C all add up to zero because we end up at the starting point. If we rearrange this algebraically by subtracting Vector A and Vector B from both sides, we end up with negative A minus B, which we can instead write as negative of A plus B. I like to write it this way because we can graphically understand this as well. We can say that, if you were to add Vector A and B together, the resultant would be this vector here. Vector C is this blue vector in the opposite direction, which is to say it's the negative of this blue vector. This blue vector is A plus B, and we're going to take the negative of that, as we've shown here, to get Vector C. The x-component of Vector C then is going to be the negative of the x-component of Vectors A and B added together. Vector A has an x-component, which is along the adjacent here. This is a subscript x, and that's the adjacent leg of this right triangle. We use cosine then to figure out its length. We have Vector A multiply by cos 21 and vector B is going to be the opposite leg of this triangle. This vertical one is B y, and this little bit here to the left is B x. That's going to be the length of be multiplied by sine of 11. This is, by the way, this is to the left, we can see that this component B in the x direction is to the left, and the left is our negative x direction. That's why there's a minus sign there. We have negative of 80 meters times cos 21. This is a positively directed x-component for Vector A. Then minus 105 meters times sine 11, and that works out to negative 54.651 meters. This part in the bracket works out to a definite positive because it's going to be up to here. This is A x minus B x will end up this length. This is the x-component of adding A x plus B x. Then we want to take the negative of that to get turned it into the x-component of Vector C. We want to turn this vector around and make it point this way. That's C x. Then we'll do the same sort of thing for the y direction. The y-component of Vector C then is the negative of the y-component of A plus the y-component of B. The y-component of A we can see is pointing down. This is A y. For that reason, we have this minus sign here. The y-component of B is a very large upwards vector. That's 105 meters times cos 11 being the adjacent side of this triangle. We have 105 meters length of B times by cos of 11 gives us B y. Then we take this sum, put a negative in front of it, and we have negative 74.401 meters is the y-component of Vector C. To figure out the length of Vector C then, we take the square root of its x-component squared plus its y-component squared. That is square root of negative 54.651 meters squared plus negative 74.401 meters squared, giving 92.316 meters. Then the direction we're asked to find theta here, an angle that is to the south of West, so we'll-- Let's erase some of this clutter here. What we now know is the x-component of C along here and the y-component of C is negative down here like this. To figure out theta, we'll take the inverse tangent of the opposite leg of this right triangle divided by the adjacent leg. We're taking the inverse tangent of C y over C x. We can ignore negative signs now because negative just tell us about directions and we already understand that this is directed to the south of west. We have been inverse tangent then of the y-component 74.401 meters divided by the x-component 54.651 meters, which is 53.7 degrees south of West. Our final answer then is that the third side on this triangle fence enclosure is going to be 92.3 meters, 53.7 degrees south of West.
Comments
You go from saying that Cx = -(Ax + Bx), then right after that input it as -(A cos21 – B sin11). Why did you switch the sign inside the parentheses from plus (addition) initially to minus (subtraction) right after that. Doesn't make sense
I'm confused why there is intermixing of the X and Y components for A and B. To me the textbook shows Rx=Ax+Bx. Just confused on why its 80cos(21)- 105sin(11) instead of 80cos(21) + 105cos(11)
Thanks
Im confused as to why the answer is south of west. Shouldn't it be north of east?