Question
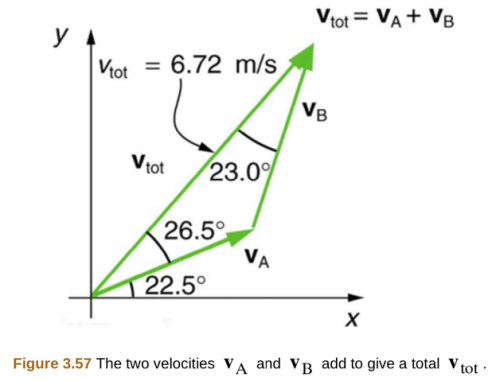
Find the components of along a set of perpendicular axes rotated counterclockwise relative to those in Figure 3.55.
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 12 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
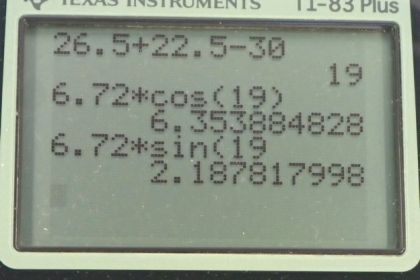
Calculator Screenshots
Video Transcript
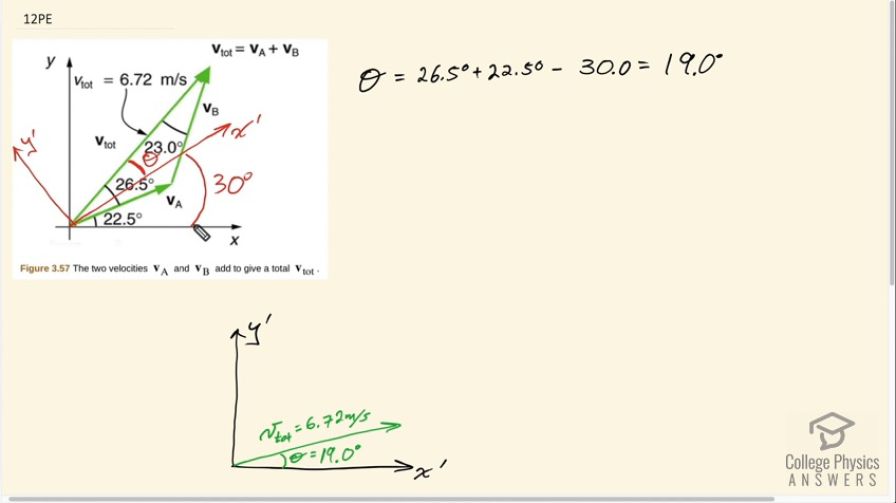
This is College Physics Answers with Shaun Dychko. We want to figure out the components of this V total vector along a set of axes that are rotated counterclockwise 30 degrees. We call it y prime here, and x prime for this axis. This is at 30 degrees with respect to the original x and y axes. I'm going to redraw this V total with the new axes down here. We're more used to seeing the y-axis straight up on the x-axis straight to the side. This is the same y prime and x prime just drawn straight up into the side. There's a 90-degree angle in here, because we know that the total angle between V total in the original x-axis is the sum of 26 and a half and 22 and a half. From that sum, we have to take away the 30 degrees of rotation here of these new axes and this worked out to 19.0 degrees, it's this angle here. The component along the x prime axis is going to be cosine of this angle multiplied by this hypotenuse, the hypotenuse of this right triangle, in other words. We're finding V total x prime. Then this vertical component here will be the total y prime. This is the adjacent leg of this triangle and so we're using cosine multiplied by the hypotenuse to find it. Cos 19 times 6.72 meters per second is 6.35 meters per second. To find the component along the y prime axis, we use V total multiplied by sine theta, so it's 6.72 meters per second times sine of 19, which is 2.19 meters per second.