Video Transcript
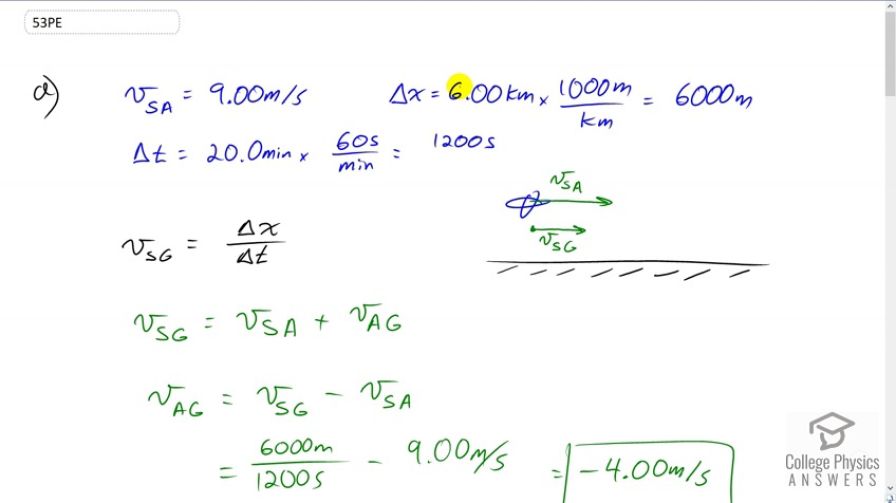
This is College Physics Answers with Shaun Dychko. We have a seagull moving at a speed of nine meters per second with respect to the air and we’re also given the distance that the seagull covered at six kilometers in a time of 20 minutes. Now one thing to keep in mind whenever I do this addition of velocity questions is that I always write two subscripts for every velocity. The first letter is mentioning the thing that’s moving, and then the second letter is what the movement is compared to. In this case it’s the seagull that’s moving and compared to the air, so it’s the velocity of the seagull with respect to the air, and we’re told that that’s nine meters per second. This distance and this time, we need to convert these into meters and seconds because we always want mks units in most of our questions, meters, kilograms, seconds, because we’re gonna be combining values together and so the units have to correspond. So we’ll convert the six kilometers into 6000 meters and the 20 minutes times 60 seconds per minute makes 1200 seconds. What is the velocity of the wind, is the question. Basically we’re given the velocity of the seagull with respect to the ground in a roundabout way because we can calculate it based on the distance travelled and the time it takes. We’re explicitly given the velocity of the seagull with respect to the air and what we want to find out then is what is this velocity of the air with respect to the ground. I suppose I can’t really draw this vector yet because we haven’t technically calculated it yet but we can assume that since the, well actually we can’t assume very much. Anyway let’s proceed through the work here and we’ll see that this vector happens to be correct. Now the velocity of the seagull with respect to the ground is gonna be the velocity of the seagull with respect to the air plus the velocity of the air with respect to the ground. I know that these subscripts are correct because when the inner subscripts are the same when you’re adding vectors, then the inner subscripts cancel and you’re left with the outer subscripts. So when you add the velocity of xy plus the velocity of yz, you’re gonna end up getting the velocity of the outer subscripts x with respect to z. The y is cancelled, so to speak. The velocity of the seagull with respect to the ground is the velocity of SA plus velocity of AG. And so now we have velocity AG, which is what we want to find and we’ll get it by subtracting velocity of the seagull with respect to the air from both sides, and then switch the sides around. And then vAG then is vSG minus vSA. We have vSG and vSA here anyway, and so we’ll subtract them. If you wanna subtract them graphically, it would look like this, it would be vSG which is a bit short, and then minus means add the opposite and so we’ll take vSA and point it in another direction and it’s longer than vSG. This is the negative of vSA and then this result is gonna be something pointed to the left since the left vector is longer than the right vector. I guess that may be confusing because this one is on the right but ya it’s pointing to the left, and it’s longer than the vector pointing to the right. Here we have 6000 meters divided by 1200 seconds is the velocity of the seagull with respect to the ground, and then subtract from that nine meters per second, the velocity of the seagull with respect to the air, and this gives negative four meters per second, is the velocity of the air with respect to the ground. Then in part b, in this case the seagull turns around and this picture should be changed here actually, the seagull is going to be moving this way. Now the time it takes to go back is going to be the distance, which we know is 6000 meters divided by the velocity of the seagull with respect to the ground which will be different in this question and we’ll calculate it by taking the seagull with respect to the air plus the velocity of the air with respect to the ground. Notice that the inner subscripts are the same, so they cancel and that means the sum will give us what we want, the seagull with respect to the ground velocity. The seagull is now moving to the left, so it’s negative nine meters per second, and then plus the velocity of the air with respect to the ground, also being negative, and this gives a total velocity of negative 13 meters per second, velocity of the seagull with respect to the ground. The negative 6000 meters displacement, negative because it’s to the left, divided by negative 13 meters per second, gives 462 seconds is the time it will take for the seagull to come back. So part c asks us to compare the total time that takes the seagull to go, let’s draw a little picture quickly. The seagull goes 6000 meters and then turns around and comes back 6000 meters. The t total is the total time for this trip, so we have delta t1 on the way there against the air, and then delta t2 with the air, with the wind on the way back. Compare that total time to the time it would take to make the trip if there is no wind, and we’ll show that when there is wind, the total time will always be more than the round trip with no wind. So we have the displacement in the first case going against the wind I should say, well doesn’t really matter. Anyways, so we have the displacement in the first case, we’ll say going against the wind is gonna be that displacement divided by the velocity of the seagull with respect to the air plus the velocity of the air with respect to the ground. And then add to that the same kind of thing for delta t2 where we have a new velocity of the seagull with respect to the air and a new displacement but they are not really that new, they are of equal magnitudes, just opposite directions and so delta x1 is the negative of delta x2 and vSA1 is the negative of vSA2. So there is no need for subscripts at all, so we’ll replace delta x1 with just delta x and then delta x2 replacing with the negative of that. And likewise for vSA1, we’ll just call it vSA and vSA2 we’ll say it’s the negative of that. We’ll factor out the common delta x. I should probably tell you a little bit about where we’re heading with all this, so you know why we’re doing this work. We’re comparing with this. This is the total time it takes when there is no wind, it’s going to be just two times the distance divided by the speed at which the seagull covers that distance. And this velocity of seagull with respect to the air is the velocity of the seagull with respect to the ground because there’s no wind. So we’re trying to create an expression for the total time with wind and we’re gonna compare that to this expression for total time with no wind. Where we are up here, we replaced the subscripts 1 and 2 with things with no subscripts and negative signs where needed and factor up to delta x. We’ll combine these fractions by finding a common denominator and that will be vAG squared minus vSA squared. We’ll multiply this first fraction by the difference, vAG minus vSA, top and bottom, and that gives these two terms there and then on the right hand term, we’ll multiply top and bottom by vAG plus vSA. That gives, the denominators will be the same because it’s, you know a binomial with a plus and then the same binomial with a minus. That makes, this is like, this is called factor in the difference of squares but kind of doing it backwards. We have a binomial, one with a plus and one with a minus, and that gives the difference in the two terms, the squares of the two terms. You can verify that by multiplying through here using the, well distributing into the brackets and multiplying through the other. What do we have here. This minus here gets multiplied by both terms in the bracket, making both of them minus, and there we have that line. Then, we see that we have vAG positive and vAG negative, and so they make zero. And then we have these like terms, and so that makes negative two times vSA and then we’ll multiply it by delta x and we get this line here. And it’s just nicer to have a fraction with no negative on the top so I multiply top and bottom by negative one to get this line here, where on the bottom we exchanged the terms. vSA squared now becomes positive and the vAG squared now becomes negative and on the numerator it’s positive. Now let’s compare this expression for the total time it takes to do the round trip with wind with this expression for the total time it takes with no wind. We have to show that delta t total is more than delta t no wind nw. So we have this expression for the total with wind and this expression for the total with no wind and we’ll multiply both sides by vSA over two delta x. The two delta xs cancel everywhere, and the vSA cancels on the right side as well, leaving the number one on the right side, then on the left we have vSA squared on top divided by vSA squared minus vAG squared. Then we’ll multiply top and bottom by one over vSA squared and on the top that bit makes one, then the bottom the first term becomes one, and then minus vAG squared over vSA squared. And so, is this thing here greater than one. The answer is yes it is. Because we know that the velocity of the seagull with respect to the air has to be greater than the size of the velocity of the air with respect to the ground because if that were not true, the seagull would not be able to do the round trip at all. Because when they’re going into the wind, in order for them to make any forward progress, they have to have a greater speed than the wind is. So we know this is true, and that being true means the square of vSA will be greater than the square of vAG and so that means the denominator here is bigger than the numerator of this fraction, and since that’s true, that makes this fraction less than one. And with that being less than one, but greater than zero, we have one minus that number, means this difference is less than one, and so one divided by a number less than one is greater than one. And so we’re showing that the total time it takes to do a round trip with wind is always going to be greater than the total time it takes to do a round trip with no wind.