Question
Show that the order of addition of three vectors does not affect their sum. Show this property by choosing any three vectors , , and , all having different lengths and directions. Find the sum then find their sum when added in a different order and show the result is the same. (There are five other orders in which , , and can be added; choose only one.)
Final Answer
please see the solution video.
Addition is commutative! (the video explains that formal term at the end)
Solution video
OpenStax College Physics, Chapter 3, Problem 8 (Problems & Exercises)
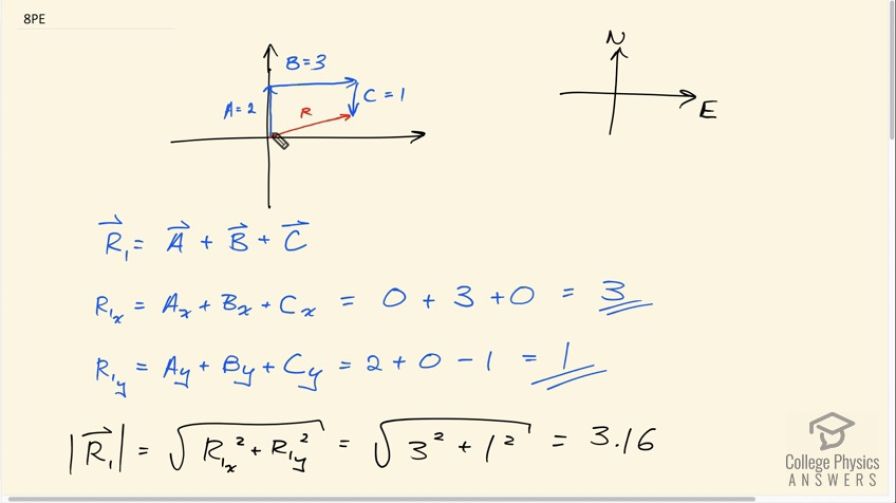
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
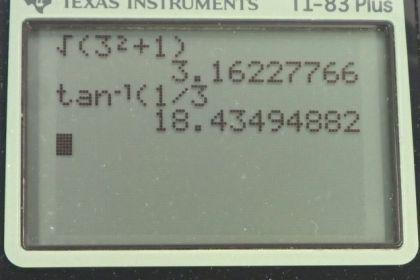
This is College Physics Answers with Shaun Dychko. We're going to show that the order that vectors are added in doesn't change the resultant. I've chosen three vectors here. We have vector A which is two units up, vector B three units across and vector C, one unit down. They're all at right angles to make our addition a little bit more convenient. The resultant in this first case is going to be vector A plus B plus C. It's x-component is going to be the x-component of A plus the x-component B plus the x-component of C. A and C have no x-components, only B does, and so our answer is three. For the y-component of this first resultant, it's going to be two units for vector A, zero units for vector B, and minus one unit for vector C, and that gives a total of one. The length of this resultant in the first case is the square root of its x-component squared plus its y-component squared, which is the square root of three squared plus one squared, which is 3.16. Its direction, which is called theta 1 is going to be the inverse tangent of its y-component divided by the x-component. It's the inverse tangent of 1 divided by 3, which is 18.4 degrees. This is a standard position angle measured with respect to the positive x-axis. You could say north of East if you like as well. So vector R one is 3.16 units, 18.4 degrees north of East. Then we're going to rearrange the order of these vectors for this resultant number two. We're going to say let's go along vector B first, so that's three units to the right and then go along vector A, which is two units up, and then vector C one unit down, and we'll see how this resultant compares with the resultant in the first case. Likewise, the x-component is of the resultant is the sum of the x-components of the vectors we're adding together. B has an x-component of three, A has none, and C also has none, so that's a total of three. The y-component of the resultant could be zero plus two minus one, which is one. These components are the same as we found before. When we add them together using Pythagoras, we get 3.16 as the length and the direction is the inverse tangent of the same numbers that we had before 18.4 degrees north of East, and so resultant of the second case is the same as resultant in the first case. This is demonstrating a property called commutativity. Vector addition is commutative. This word commutative means you can move the terms around and still get the same answer. It comes from the word commute, which you know commuting to work, moving around, so you can move around terms and addition is commutative. Division is not commutative and neither subtraction because you can't say that two minus one is the same as one minus two. That's not true. You can't move terms around with subtraction. Subtraction is not commutative. Because on the left hand, you have positive one, on the right hand, you have negative one, those are different answers. But vector addition is commutative.