Question
An athlete crosses a 25-m-wide river by swimming perpendicular to the water current at a speed of 0.5 m/s relative to the water. He reaches the opposite side at a distance 40 m downstream from his starting point. How fast is the water in the river flowing with respect to the ground? What is the speed of the swimmer with respect to a friend at rest on the ground?
Final Answer
,
Solution video
OpenStax College Physics, Chapter 3, Problem 65 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
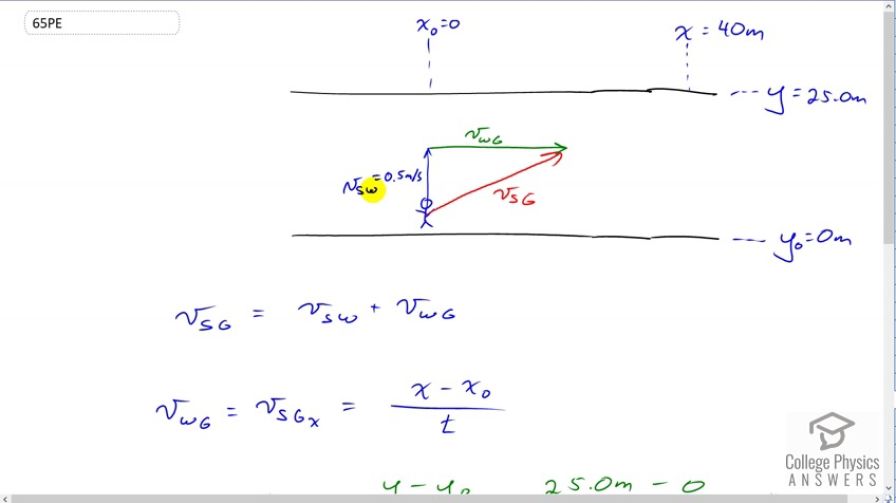
This is College Physics Answers with Shaun Dychko. This swimmer is travelling across the river and a speed of 0.5 meters per second with respect to the water, so I’ve written v subscript S for swimmer and then W for water. There’s also a current that is perpendicular to the swimmer’s velocity and the current is the velocity of the water with respect to the ground and it’s going downstream, this way to the right. Here’s the resultant velocity of the swimmer with respect to the ground so that they will end up over here, 40 meters downstream from the position that they started with. We’re told that the river is 25 meters across, so we have an initial y position of zero and a final y position of 25. Our job is to figure out what is this velocity of the water with respect to the ground. Well that velocity is the same as the velocity of the swimmer with respect to the ground’s x component because this velocity here has no x component and this one is entirely in the x direction. And that will be the displacement in the x direction divided by the time it takes to do this displacement here, but we don’t know what that time is. So let’s figure out that first, using the y dimension and then we’ll plug that back in here to figure out the speed of the water. So the time it takes to cross is the width of the river 25 meters divided by the y component of the swimmer’s velocity with respect to ground. It has to be with respect to ground because this dimension is with respect to the ground as well. So that’s 25 meters divided by 0.5 meters per second, which is 50 seconds. So we plug 50 back in for t, and we get the velocity of the water with respect to the ground is 40 meters divided by 50 seconds which is 0.8 meters per second. The speed of the swimmer with respect to somebody standing on the shore is the velocity of the swimmer with respect to the ground. So that’s the square root of its components squared added together, and those components as we mentioned before are the velocity of the swimmer with respect to the water and the velocity of the water with respect to the ground. So square those components, add them together, take the square root of the sum and then you get 0.94 meters per second is the velocity of the swimmer with respect to the ground. Well I suppose that’s not quite the velocity technically because I didn’t find the angle here but the question doesn’t ask us to so we’ll stick with this as our answer, this is the speed of the swimmer with respect to the ground.

