Video Transcript
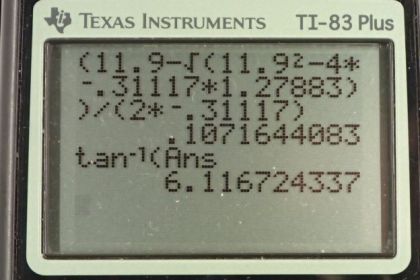
This is College Physics Answers with Shaun Dychko. This tennis player is going to serve this ball such that the ball just barely goes over this net. So when the ball travels horizontally 11.9 meters which is the distance between the service line and the net, the ball's height should be 0.91 meters above the ground. We're told what the speed of the ball is, it's 170 kilometers per hour which we'll convert into meters per second by multiplying by one hour for every 3600 seconds and then by 1000 meters per kilometer and the kilometers cancel and so do the hours leaving us with meters per second. So it goes at 47.222 meters per second. But we don't know the angle and so, part one of this question is to figure out what should this angle be such that the ball just barely goes over the net. Then the second part of the question will be, well, with the ball on that trajectory, will it go past the service box or not? So will it get this server a point or will it be -- what do they call it -- a let? No, a let is if it hits the net. Anyway, so yeah. We'll see if this service can get it into the service box or not by checking to see whether the range of the ball is less than the position of the service box on the opposing side of the net. So this service box we're told is 6.4 meters from the net and so we add that to the distance from the net to the service line and we get 18.3 meters is the position of the end of the service box on the opposing side. So fasten your seat belt, there is some serious algebra in this question. You have to know some trigonometric identities and -- but you know, we'll make it through. So just stick with me here. We want to find out what the y position is at the net, so we put a subscript n for net and it's going to be the initial y position which we're told is 2.5 meters high, plus the initial y component of the ball's velocity, times by the amount of time it takes to get to this position of the net, plus one half times the vertical acceleration, multiplied by the time to the net squared. Then I'll make a substitution for the y component of the initial velocity and that's going to be the initial speed multiplied by the sine of this angle theta which we don't know but we're going to figure it out. We're using sine because that is the opposite leg of this right triangle here. Then I just repeated that part there. So, that's as much as we can do with our vertical formula. There are two unknowns in this equation. There is the theta which we don't know and there is the time it takes for the ball to get to the net which we also don't know. So if you have an equation with two unknowns, you can't solve it and it means you need another equation in order to make a substitution for one of these unknowns. Or you could add two equations as well and so on. There's other methods of combining simultaneous equations but we're going to do the method of substitution in this solution. Okay. So I use the word simultaneous equation to say that sometimes if you have multiple unknowns here, you need to have another equation that describes the same situation. A collection of equations that all describe the same thing are called simultaneous equations. So we're going to consider the horizontal direction now. So we have the x position of the net, there's going to be the initial x position of the ball plus the horizontal component of the ball's initial velocity multiplied by the time it takes to get to the net. x naught is zero because it starts -- we'll say that the beginning position is zero, we can just state that if we like, and that makes this equation reduced to this where I've substituted for v naught x with v naught cos theta because v naught x is the adjacent leg of this right triangle. We can solve this for t n and we call that equation two and this is useful because we're going to substitute it up here into equation one. So before we get ahead of ourselves, let's divide both sides by v naught cos theta here and then switch the sides around and we get tn is the x position of the ball when it's above the net divided by its initial speed that's costheta. Okay. So, substituting equation two into equation one to get rid of one of the unknowns, we don't know what tn is and so, we're going to substitute it with things that we do know plus the thing we're trying to find. So tn we don't actually know from this equation because we don't know theta but it’s a useful substitution to do because then on this line here, you'll see that we have an equation consisting of only one unknown and that being theta. So this is equation one repeated but I have replaced every instance of t subscript n with this fraction xn over v naught cos theta. Then this sine -- so there's some work to do here right, 'cause you have to -- we're trying to find out what is. But theta is contained within these trigonometric functions and so it's going to be a bit of a trick to get it out of there. So we're going to simplify this. Sine theta over cos theta, there's a trigonometric identity which says sine over cos theta is tangent theta and so that's what I've done here. I've written tangent theta instead of sine theta over cos theta and also canceled the v naught on the top and bottom of that fraction so we have tan theta times xn. Then on this term here, I've squared this fraction so we have xn squared times by ay over two times v naught squared times cos squared theta. Now, we have theta in the tangent function there and we have theta within cos squared there. So what we want to do is use trigonometric identities to have only one type of trigonometric function. We want just tangent. It turns out that one over cos squared theta is the same as one plus tan squared theta. We can verify that's true up here, why don't we do that? So we have one plus tan squared theta and that is one plus -- now tangent theta is sine over cosine, that's kind of its definition so we'll say this here. So tan squared theta is sine squared theta over cos squared theta and then if we want to add these two things, that's one plus this fraction, we can multiply the one by cos squared over cos squared theta giving us the next line which is cos squared theta over cos squared theta plus sine squared theta over cos squared theta. Now because the denominators are the same we can add the numerators. Cos squared theta plus sine squared theta all over cos squared theta but cos squared plus sine squared is the pythagorean identity and it is the number one. So we end up with one over cos squared theta. There we go. We have verified that one plus tan squared theta is one over cos squared theta. So, we can replace this with this in other words. Now, it looks weird a little bit but it is a quadratic equation. We have you know, tan squared theta -- it's kind of a funny way that they write the square of a trig function. It also could be written as this, tan theta squared. So it's a variable squared just as in ax squared plus bx plus c equals zero. That's the traditional way to write a quadratic equation. It's a thing squared and in this case it's called tan theta instead of x, plus some factor times the thing to the power of one, and then plus some constant terms. So we're going to expand this bracket by multiplying through by this factor outside and then we'll write our squared term first, just so that it looks the way that we're used to for a quadratic equation. So we have ay xn squared over two v naught squared times tan squared theta minus xn multiplied by tan theta. I just switch the order of the factors around, no big deal, and then plus this multiplied by one here, and minus yn so I subtracted yn from both sides, the height of the net. Then plus this initial height of the ball and all that equals zero. So then we plug in all the numbers. We have the acceleration due to gravity, the height, the horizontal position of the net squared, divided by two times the initial speed of the ball and then that's the factor in front of the squared term; then we have the position of the net and then plus acceleration times horizontal position of the net squared over two times its speed squared, minus 0.91 meters height of the net, plus 2.5 meters initial height of the ball when it's being served. All this works out to this equation. Now, we have coefficients that we can plug into our quadratic formula to solve for tan theta. It gives two answers, one is 0.10716, it also gives an answer negative 38 which we will reject and I'll tell you why in a second. So theta then is going to be the inverse tangent of this tangent and that gives us 6.1 degrees. Now the reason we rejected the negative 38 for tan theta is because that would give an angle of 80 something degrees or so and that would be corresponding to hitting the ball at an angle like this so that it has this trajectory and it just goes blunk, right on the other side of the net. That's not the kind of serve that a tennis player is going to want to do because then the opponent could hit this lob real easily and that would be bad. So we're going to take this solution because that is the strategic approach for this tennis player, is to shoot the ball in this trajectory here which is the other one that just clears the net. So there's two ways he could hit the ball such that it just barely goes over the net given that initial speed and we're going to choose this one because that's the way to do it in order to win. So the next part is to see whether or not this ball lands within the service box. So does it hit somewhere here is the question, somewhere before xs, s for service box. We're going to figure out how long the ball spends in the air before it hits the ground and then we'll plug that into this formula for the x position when it hits the ground. So the x position is its initial x position which is zero, plus the initial x component of its velocity which, you know, we don't really need to say initial because it has a constant x component of its velocity anyway, and then multiply that by the amount of time that is spends in the air. So this, because this x naught is zero, this reduces to v naught times cos theta times the time, being the horizontal component of its velocity. So, to figure out the time it spends in the air though, we need to use this formula for the vertical dimension and we'll subtract y from both sides. Although actually, it's just the number zero isn't it? Because it hits the ground and we've defined the ground to be zero so we don't need to think about that variable anymore. So we have one half ay t squared and then I put a minus v naught sine theta t because this vertical component of its initial velocity is directed downwards and so I'm putting a minus in front of it for that reason. Then it's the opposite leg of this velocity triangle so we use the sine function multiplied by the hypotenuse to get it. Then we plug in numbers and then we solve this quadratic equation. So we have one half times the acceleration, times time squared minus the initial speed, multiplied by sine of the angle of it being hit and that is what we found in part A. Then plus 2.5 meters and all that equals zero and so we have negative 4.9t squared minus 5.0317t plus two and a half equals zero and so that's a quadratic equation for which we use the quadratic formula to solve. This gives two answers, one being positive and the other being negative. Negative time has no physical interpretation here so we take the positive one. Then we plug that time in for our formula for the x position when it hits the ground. So we have 47.222 meters per second, times cosine of the launch angle 6.1167 degrees, times 0.3623 seconds that we just determined before, and that gives 17.0 meters. Because that 17.0 meters is less than the 18.3 meters, so it's going to hit about here say, because it's less than the 18.3 meters for that reason, yes the ball lands in the service box.