Question
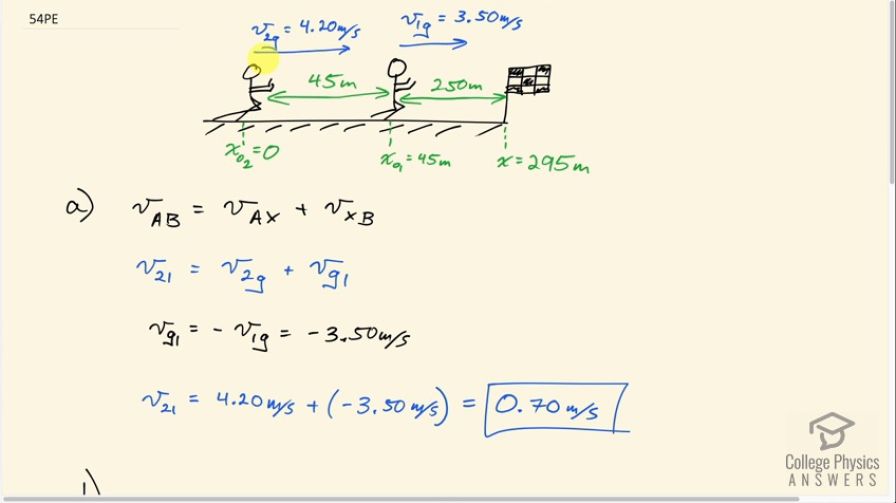
Near the end of a marathon race, the first two runners are separated by a distance of 45.0 m. The front runner has a velocity of 3.50 m/s, and the second a velocity of 4.20 m/s. (a) What is the velocity of the second runner relative to the first? (b) If the front runner is 250 m from the finish line, who will win the race, assuming they run at constant velocity? (c) What distance ahead will the winner be when she crosses the finish line?
Final Answer
- The second runner will finish first.
Solution video
OpenStax College Physics, Chapter 3, Problem 54 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
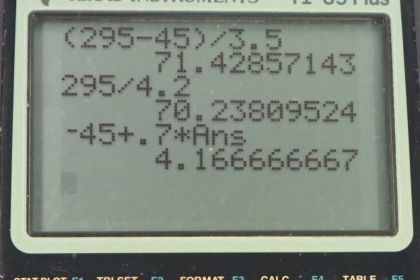
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a race in which there are two runners; runner number one is 250 meters from the finish line and runner two is 45 meters behind runner one. And this allows us to write down what their positions are. So the position initially of runner two, we'll call zero which would make the position initial of runner one, 45 meters and the finish line then will be this position x, the final position for either of them, 295 meters. And now question A asks us what is the speed or velocity of runner two with respect to runner one? Now both of the velocities given to us implicitly are with respect to the ground. And so, and I wrote that explicitly here by writing this subscript g after the number one, where the subscript g after the number two. Because here our answer to part A will be the velocity of subscript two with respect to subscript one. That is the velocity of runner two with respect to runner one. And we follow this pattern of adding relative velocities, where if you want the velocity of a with respect to b, which is runner two with respect to one in our case. a is two and b is one, then you have to set up velocities such that you have the first subscript with respect to something, plus the velocity of that same something with respect to the second subscript you want. So x in this case is the ground. And so you wanna have the velocity of runner two with respect to the ground which we're given, plus the velocity of the ground with respect to runner one, which we're not exactly given. We're given the velocity of one with respect to the ground, but the velocity of the ground with respect to runner one is gonna be the negative of velocity of runner one with respect to the ground. So that’s negative 3.5 meters per second. So this is what we can plug-in for v g one, negative 3.5. And we end up with velocity of runner two with respect to one is 4.2 meters per second, minus 3.5. Which is positive 0.70 meters per second. And this positive answer means that runner two is catching up to runner one. Because to the right is the positive direction in our picture. Okay, and then part B asks who will finish first? So the final x-position of something moving is it's initial position plus it's speed times time. That’s equation 50 from chapter two. And we can solve for t by subtracting x naught from both sides. And then dividing both sides by v, after switching the sides around. And we have final position minus initial position divided by speed. And so the final position will be the finish line, which is at position 295 meters. And for runner one, their initial position is 45 meters. So we have 295 minus 45 divided by the velocity of runner one with respect to the ground which is 3.5 meters per second. Which gives the time of 71.43 seconds. The time for runner two to reach this final position of 295 meters, is going to be only 70.24 seconds. And so runner two will finish first. Because it takes them less time to get to this position of the finish line. Now part C asks us, by how much will runner two be ahead of runner one when runner two finishes? And there's a couple ways to answer this; one is you could say, well, how far will runner one go in this amount of time? Because this is the time when runner two finishes. And so where will runner one be at this time? That's not the method I use though instead I said, well, here's the position of runner two with respect to runner one, here's the initial position of runner two with respect to runner one, which is negative 45 meters. Because runner two is 45 meters behind runner one. And then add to that the velocity of runner two with respect to one which we found in part A, multiplied by time which is the time it takes for runner two to finish. So that's negative 45 meters plus .7 meters per second times 70.2381 seconds, which is 4.17 meters.