Question
Find the components of vtotv_\textrm{tot} along the xx and yy axes in Figure 3.55.
<b>Figure 3.55: </b> The two velocities v_{A} and v_{B} add to give a total v_{tot}
Figure 3.55: The two velocities v_{A} and v_{B} add to give a total v_{tot}
Question by OpenStax is licensed under CC BY 4.0
Final Answer

vtotx=4.41 m/sv_{tot_x} = 4.41 \textrm{ m/s}

vtoty=5.07 m/sv_{tot_y} = 5.07 \textrm{ m/s}

Solution video

OpenStax College Physics, Chapter 3, Problem 11 (Problems & Exercises)

OpenStax College Physics, Chapter 3, Problem 11 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 3, Problem 11 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. Our job in this question is to find the x and y components of this vector, the total vector, the resultant of Va plus Vb. It has components along the x axis, here's the x component of the vector and then here is the y component of the vector. Right here, this is V total y component, the amount by which the resultant goes up. Then along here horizontally, we have V total x, the amount by which this yellow vector goes to the right. To find the x component, we're going to need to know what this angle is in here and then we'll use cosine multiplied by the hypotenuse to find the length of this adjacent leg of this right triangle. So to find this angle we have to add the 26 and a half to the 22.5. That gives us 49 degrees and so the x component of the total then is the length of the vector, 6.72 meters per second, multiplied by cosine of 49. That gives 4.41 meters per second. They component of the V total is going to be 6.72 meters per second multiplied by sine of 49 degrees, and we're using sine because this is the opposite leg of the triangle. We use sine always to get the opposite leg of a triangle, multiplied by the hypotenuse and that gives 5.07 meters per second.

Comments

I don't think this answer is right

how do you know to use 49 degrees for both the x and y components? why not the 23 degrees?

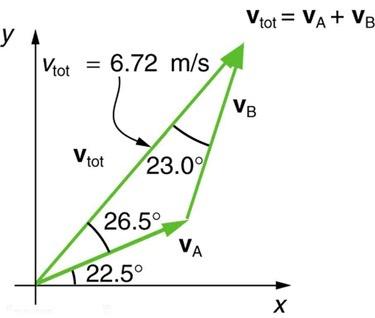
When finding components we want to imagine a right triangle (a triangle with a 90∘90^\circ angle, in other words) that has the vector as it's hypotenuse (which is the name of the longest side opposite the 90∘90^\circ angle), and the components are the legs. When the legs of the right triangle are parallel to the x and y axes, we call these legs x and y components along these axes. All this is to say that the 49∘49^\circ angle is the angle in the imaginary right triangle with legs parallel to the x and y axes. It's the angle between the vector and the x-axis. Using 23∘23^\circ would find components along different axes.

How can you use this to find the magnitudes of velocities for vector A and vector B?

Knowing the components of the resultant isn't actually useful for finding the magnitudes of vectors A nor B. This is because vectors A and B could have a variety of different lengths, but with adjusted angles, they could nevertheless create the same resultant.
Nevertheless, since so many angles are given in the problem, you can figure out vector A and B magnitudes, you just can't do it with the resultant components. I would figure out the third angle inside the vector triangle (the three are supplementary), then use the sine law to find the lengths of vectors A and B.

I'm not coming up with the same answer when putting the equation in?

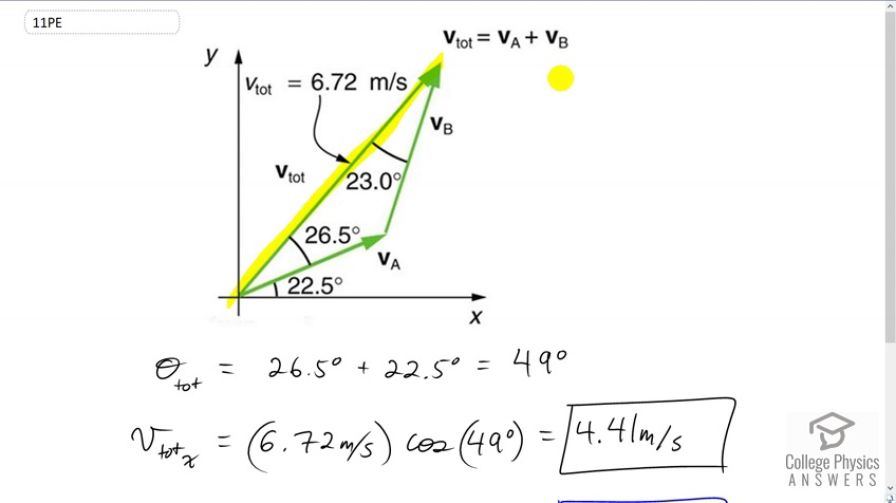
Keep in mind that we're finding the components of the resultant vector (it's a bit confusing that the picture has three vectors on it, so let's be sure we're looking at the right one. It's labeled vtotv_{\textrm{tot}}). Have you looked at the calculator screenshot showing how I plugged this into the calculator? Are you seeing anything different on your calculator, or something amiss with how I've plugged values into mine?

Hey check this out. So I'm following along your video instructions and the calculator screenshot-- i'm plugging in my assignment numbers (vtot=6.44 and o=23.5- instead of 6.72 and 22.5)
Consistently, I was coming up with the wrong answer. So then I checked your calculations... and google calculator gave me a different calculation of 6.72*cos(49) = 2.01998189396

Turns out... your calculator is right, and the scientific calculator online that i was using, was not accurate! This is the link. I wish I could show you a screenshot. I ended up using a different calculator, and it came out the same as yours.
https://www.google.com/search?q=scientific+calcultor&rlz=1C1RAEH_enUS88…

I learned today from my prof. that the scientific calculator can give you wrong answers when in the wrong mode. If you are using Casio make sure to look at the top and you should see a D, which stands for degrees. I did not have it on and it gave me the wrong answers.

You're quite right GabiFerreira, and thank you for responding to the other student's comment. Calculators need to be told whether the angles you're entering are in degrees (for which you want the "D" you mentioned), or whether the angles are in radians.

How would you find the angle thats 22.5 if you werent given it?

No Q&As found for this question yet. How about you submit the first one?