Question
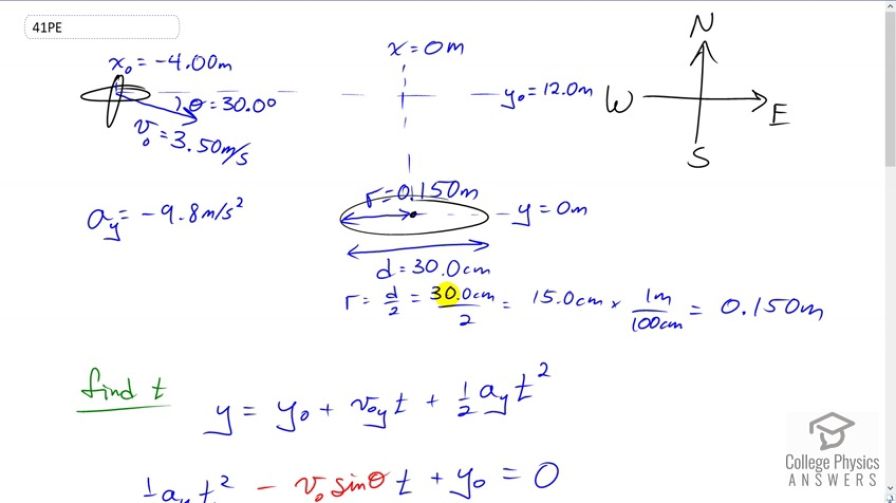
An owl is carrying a mouse to the chicks in its nest. Its position at that time is 4.00 m west and 12.0 m above the center of the 30.0 cm diameter nest. The owl is flying east at 3.50 m/s at an angle below the horizontal when it accidentally drops the mouse. Is the owl lucky enough to have the mouse hit the nest? To answer this question, calculate the horizontal position of the mouse when it has fallen 12.0 m.
Final Answer
The owl is not lucky since the mouse goes past the far edge of the nest.
Solution video
OpenStax College Physics, Chapter 3, Problem 41 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. This owl’s nest is 30 centimeters in diameter. That means the radius is half of that, so 15 centimeters and we’ll convert that into meters by multiplying by one meter for every hundred centimeters. That gives 0.15 meters. The owl is carrying a mouse, and it accidentally drops the mouse when it’s flying at a speed of 3.5 meters per second at an angle of 30 degrees below the horizontal. The question is, will this mouse when it falls, land in the nest or will it land past it or before it. That is the question. Our little owl babies gonna be hungry for a little bit longer or are they gonna get food. We’ll choose the origin to be at the center of the nest. That means the y position is zero there and so is the x position. The initial position of the mouse is at x naught, negative 4.00 meters. That’s four meters to the west of this origin, center of the nest. The initial y position is 12 meters above the nest. The acceleration in the y direction is negative 9.8 meters per second squared. That’s all the information we are given, that’s all we need to know. So to figure out where this mouse will be when it reaches this height, we need to figure out how long it’ll spend in the air by the time it gets here or, well not there necessarily but to this height anyhow. And then after we know how long it’ll take to reach the height of zero, we will use this formula to figure out what the horizontal position of the mouse will be. And then we’ll see whether or not that horizontal position is within the nest or not. The y position of the mouse is its initial y position plus the vertical component of the initial velocity times time, plus one half times the vertical acceleration times time squared. The final position is zero and because it’s the height of the nest which we’ve chosen to be zero, our reference level. We’ll substitute for the vertical component of the velocity by writing the initial speed multiply by sine of the angle of velocity there. That’s gonna be 3.5 meters per second times sine of 30. That’s multiplied by time plus the initial height and all that equals zero, as we said here. This is a quadratic equation, and we’re gonna substitute as many numbers as we know. And then we’ll use the quadratic formula to solve for t. We know the vertical acceleration is negative 9.8 meters per second squared, multiply that by half, that gives us our coefficient for the squared term of negative 4.9. The initial speed is 3.5 meters per second which we’ll multiply by sin 30 and this makes 1.75. sin 30 is a half by the way, so I didn’t take a calculated screenshot of this calculation because three and a half times a half is 1.75. Then plus 12, all that equals zero. We plug this numbers into our quadratic formula and we get 1.3965 seconds is the time it takes for the mouse to reach this height here. The next question is, where will it be horizontally. The horizontal position is the initial x position plus the horizontal component of its velocity, multiply by time. The horizontal component of its velocity is the initial speed times cos theta because we’re looking for the horizontal component of this triangle here. This is v initial x, that’s the adjacent leg of this triangle. So we use cosine times the leg of the hypotenuse which is v naught. We have negative four meters as the initial horizontal position, plus three and a half meters per second times cos theta times the time of 1.3965 seconds that we calculated earlier and that gives 0.233 meters, will be its final position. Now 0.233 meters is over here somewhere because here is x equals zero and we now have a positive x number so that means to the right of the origin. The edge of the nest is at 0.15 meters, and so 0.233 exceeds that edge position and so the mouse will miss the nest by going past it. There we go.
Comments
Where did you come up with the initial velocity x time being a negative?
my teacher got it 4.233 for x



