Question
In the standing broad jump, one squats and then pushes off with the legs to see how far one can jump. Suppose the extension of the legs from the crouch position is 0.600 m and the acceleration achieved from this position is 1.25 times the acceleration due to gravity, . How far can they jump? State your assumptions. (Increased range can be achieved by swinging the arms in the direction of the jump.)
Final Answer
Solution video
OpenStax College Physics, Chapter 3, Problem 35 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
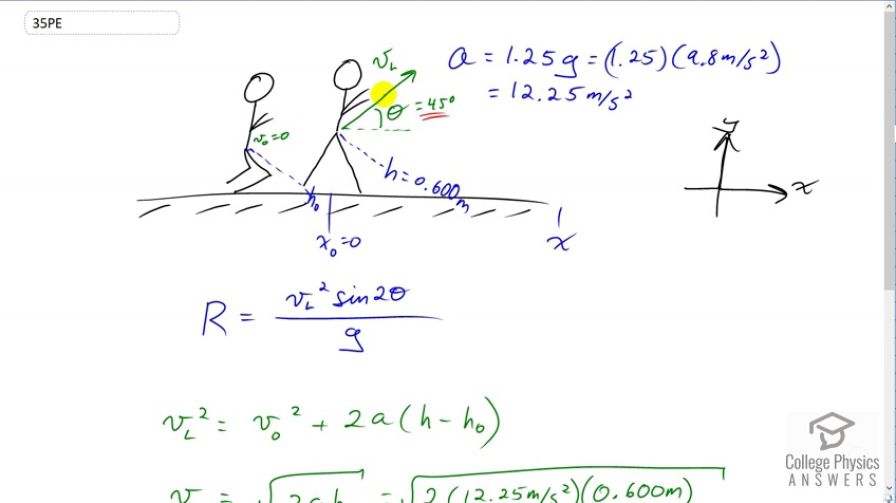
This is College Physics Answers with Shaun Dychko. We're told that this long-jumper is crouched 0.6 meters down and then they're going to extend their legs and launch themselves into this long jump. They're going to have acceleration while they extend their legs of 1.25 times g. So that's 1.25 times 9.8 which is 12.25 meters per second squared. We're asked to find out how far will they go. Now this picture is meant to show the long-jumper at two different times. This guy is meant to be in the same place as this guy. It's the same person but just at two different times. This is drawn here after the legs are extended. So, we're going to take this to be the position zero, and then they land over here somewhere, and they're going to land at the same height as they started with, so that means we can use this range formula. That is a very convenient formula, makes our work much easier. Now we're not given the angle of launch though. We can figure out what the launch velocity is based on this acceleration and knowing that it occurs over a distance of 0.6 meters. But we don't know what the angle is and we're told to make some assumptions in the question. So our assumption will be that this long-jumper will choose an angle that optimizes the range. They'll choose an angle such that the range is the greatest. Assuming no air friction, which is what we are always assuming in questions in the text book, the angle for the greatest range is 45 degrees because the sine of something can at most be one. You can never sine of anything being greater than one. So, what angle here makes a sine of one? Well the sine of 90 is one and so whatever angle makes this thing here into 90 is what will work. So we want to make that 2theta equal to 90 and we can do that by dividing both sides by two and we can see that theta is 45.So that's our assumption. The long-jumper is aware of physics and they will launch themselves at 45 degrees. Okay. So now the problem is then to figure out what this launch velocity is. So we know that the launch velocity squared is going to be the initial velocity here squared which is zero because this is a long-jumper, they start from rest, plus two times the acceleration which we are given, times the distance over which this acceleration occurs, the extension of the legs, h minus h naught, h naught being zero. So this simplifies to this line here and then we'll take the square root of both sides to get the launch velocity. The launch velocity is square root of two, times acceleration of 12.25 meters per second squared, times the extension of the legs, 0.6 meters, and that gives 3.8341 meters per second. Keeping lots of digits there because this is an intermediate calculation. Now the range is going to be that launch velocity squared, multiplied by the sine of 90 which is one, divided by 9.8, giving us a range of 1.50 meters.
