Question
Gun sights are adjusted to aim high to compensate for the effect of gravity, effectively making the gun accurate only for a specific range. (a) If a gun is sighted to hit targets that are at the same height as the gun and 100.0 m away, how low will the bullet hit if aimed directly at a target 150.0 m away? The muzzle velocity of the bullet is 275 m/s. (b) Discuss qualitatively how a larger muzzle velocity would affect this problem and what would be the effect of air resistance.
Final Answer
a) below the level of the gun / target.
b) see video for discussion.
Solution video
OpenStax College Physics, Chapter 3, Problem 39 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
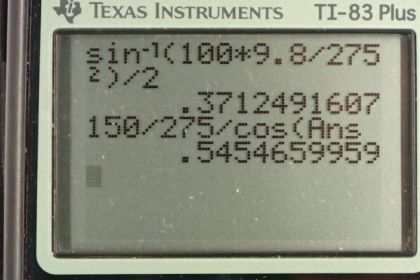
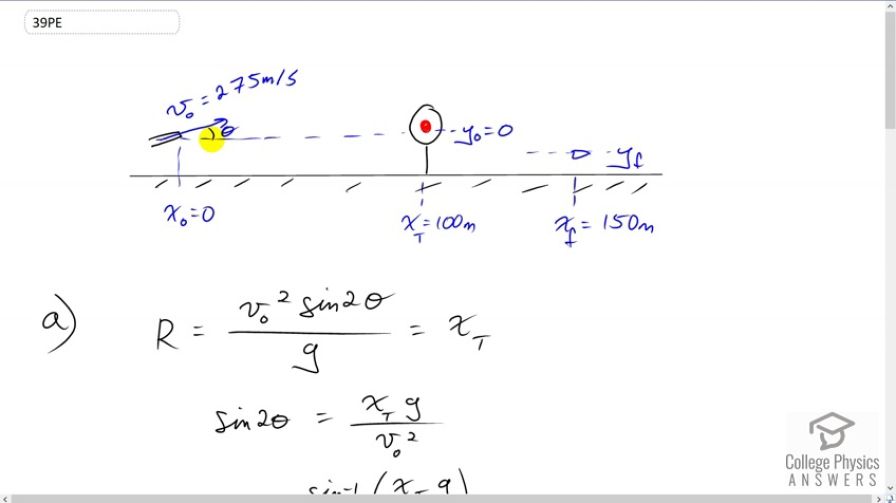
This is College Physics Answers with Shaun Dychko. The sights on this gun are calibrated such that it causes the gun to be angled upward, just slightly so that when the bullet reaches a target 100 meters away, it'll impact the target as at the same height as the gun. So because this target at 100 meters away is at the same height, we're allowed to use this convenient range formula and we're going to calculate what the angle is that the calibration of the gun sights has inclined the gun at. Then after we know that angle, and given this muzzle velocity, we'll be able to find the vertical position of the bullet at 150 meters away from the gun. We'll find that it's a little bit lower than the initial height of the bullet. So, the range is the initial speed squared times sine of two times the angle of launch, divided by acceleration due to gravity and that is xt on this graph, x subscript t for target. We're solving this for theta and we'll start by multiplying both sides by g over v naught squared, giving us this line here. Then we'll take the inverse sine of both sides leaving us with two theta on the left and inverse sine of xtg over v naught squared on the right and then divide both sides by two, giving us theta is inverse sine of the position of the target horizontally, times acceleration due to gravity, divided by the muzzle velocity squared, divided by two. So it's the inverse sine of 100 meters, times 9.8 meters per second squared over 275 meters per second squared all divided by two which is 0.37125 degrees. You can see this angle is very small so you wouldn't actually see the gun inclined the way I've drawn it but I had to do that just to explain that there is an incline there but it's a very small amount. Now knowing that angle we would like to use this formula to find the y position at 150 meters, y subscript f for final. It's equal to the initial y position plus the vertical component of the initial velocity multiplied by time plus one half times acceleration times time squared. But now we know what theta is and so we can figure out what this term should be, most of it anyhow although we don't know i>t. We've done some work to find theta but we also have to do more work to find time before we can finally use this formula for finding vertical position. So we turn to the horizontal dimension to figure out the time. We know that the horizontal final position, 150 meters away, is the initial horizontal position plus the x component of the velocity multiplied by the time it takes to get to that final position 150 meters away. I suppose I should put a subscript f on the t's there 'cause this is a final time, the time of reaching x subscript f. x naught disappeared because it is zero, it starts at horizontal position of zero. We're going to solve this for tf so divide both sides by v naught cos theta and it cancels there and switch the sides around. We have the time is the horizontal position divided by the muzzle velocity times cos theta. So it's 150 meters over 275 meters per second times cos of 0.37125 degrees that we calculated earlier. That gives 0.54547 seconds to get to 150 meters. Now finally we can use this formula although we won't actually calculate because we don't know what the height of the gun is. But we can find yf minus y naught. So we'll find out how much below the level of the gun the bullet is. So, we subtract y naught from both sides and we get this difference or this amount by which the bullet is lower than the gun equals the initial muzzle velocity times sine theta times t plus one half acceleration vertically times time squared. So now we know everything 'cause we've done lots of work to calculate all the variables in this formula. So we have 275 meters per second muzzle velocity times the launch angle of sine of 0.37125, times the time of 0.54547 seconds, plus one half times negative 9.8 meters per second squared acceleration due to gravity, multiplied by the time squared. That gives negative 0.48598 meters. The negative indicates that the vertical position of the bullet is lower than it was to begin with and it'll be 48.6 centimeters below the level of the target at 150 meters. So I said below the level of the target; I could have also said below the level of the gun 'cause the target and the gun are at the same level. Now if there was a larger muzzle velocity, that would reduce the amount of time that the bullet spends in the air and we can see that this discrepancy or this height discrepancy of the vertical position of the bullet with respect to the gun is proportionate to the square of the time and so as t gets reduced so does this difference in height. So it will fall less when it has a higher muzzle velocity as a result of reducing the amount of time that is spent in the air. Air resistance on the other hand would increase the time that the bullet spends in the air and so by increasing the time it spends in the air, air resistance would cause the amount by which the bullet drops to increase in magnitude.