Question
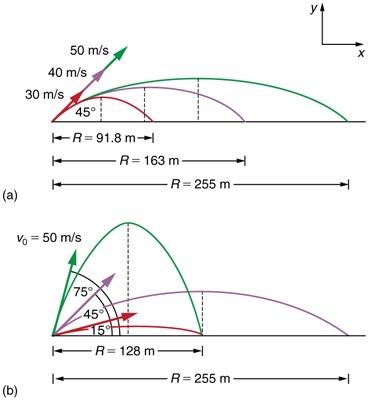
Verify the ranges for the projectiles in Figure 3.40(a) for and the given initial velocities.
Final Answer
:
:
:
Solution video
OpenStax College Physics, Chapter 3, Problem 31 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
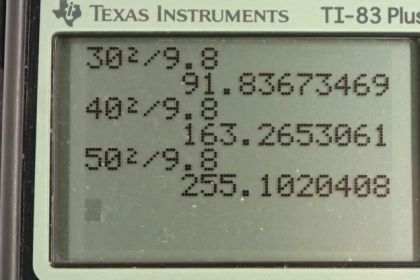
Calculator Screenshots
Video Transcript
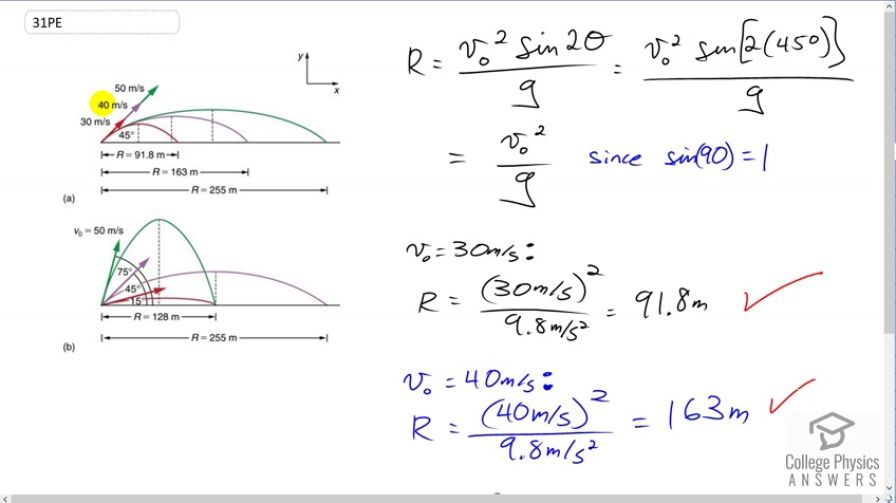
This is College Physics Answers with Shaun Dychko. We're going to verify the ranges shown in this figure for each of these different launch velocities, 30 meters per second, 40 meters per second or 50 meters per second. We're going to use the range formula which we can do because there's a nice convenience in this problem where the final height of the projectile is the same as the launch height. So because that's the case we're allowed to use this range formula. Now another convenience is that with an angle of 45 degrees when you substitute 45 in for theta, we are taking the sine of two times that which is the sine of 90 degrees in other words. The sine of 90 is one, so that means this part here is going to be one. So we can write the range formula then in this case, as v naught squared over g. So for 30 meters per second, we have the range is 30 meters per second squared divided by 9.8 meters per second squared giving 91.8 meters which does verify what's shown in the figure. Then for 40 meters per second launch velocity, we have 40 meters per second squared divided by 9.8 giving 163 meters which checks out. Then for 50 meters per second we square that, divide by 9.8 and get a range of 255 meters which also is the same as what's shown on the figure.