Question
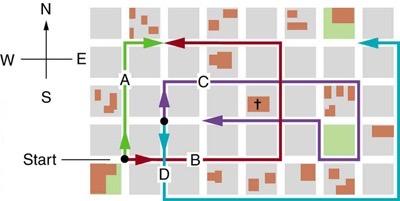
Find the following for path C in Figure 3.56: (a) the total distance traveled and (b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.
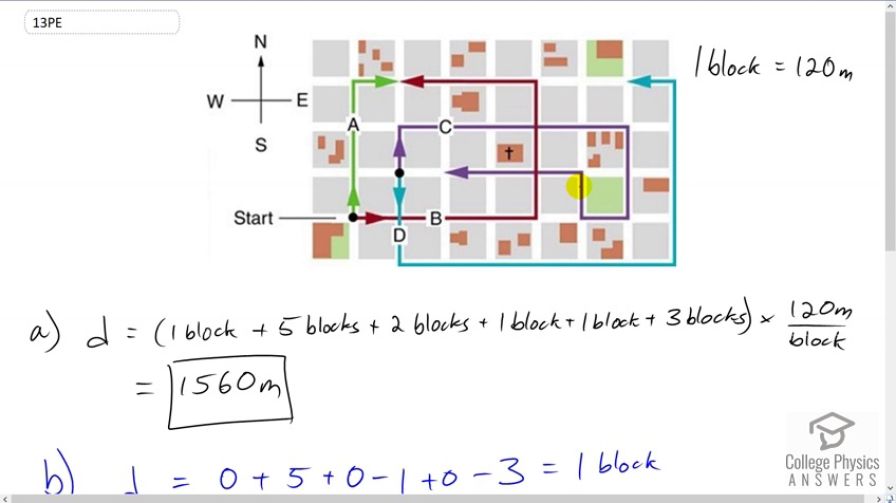
Final Answer
a)
b)
Solution video
OpenStax College Physics, Chapter 3, Problem 13 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. To find the total distance traveled along path C, we need to add the length of each part of the path or each part of the route. So we have one block going north here and then we have one, two, three, four, five blocks going to the east and then two blocks south, one block west, one block north and then three blocks to the west. So each of those numbers are written here and then we take that sum and we multiply by 120 meters per block. This gives us 1560 meters is the total distance traveled. Now for the displacement between this position and the end point, we can see that the displacement is going to be one block to the east. But the question asks us to show how we figure that out analytically instead of graphically. So we'll take the x component of the displacement as being the x component of each of these of the route. So we have zero x component at that part. This part is an x component of positive five. This part is an x component of zero, negative one x component, zero and then negative three x component. Those are each of the numbers here. That makes one block positive which is what we expected because we expect one block positive here. Then for the y components we have positive one block there and then this has no y component at all. This section has negative two for y component. This section has nothing. This has positive one block for y component and this has none. So each of those numbers are written here and that adds up to zero. So, magnitude of our displacement will be the square root of the sum of the squares of the components. That's the square root of one squared plus zero which is one. Then we'll take the angle as being the inverse tangent of the y component over the x component. So it's the inverse tangent of zero which is zero. This zero represents directly east. So our displacement is 120 meters east.


