Question
Repeat the problem above, but reverse the order of the two legs of the walk; show that you get the same final result. That is, you first walk leg B⃗\vec{B} , which is 20.0 m in a direction exactly 40∘40^\circ south of west, and then leg A⃗\vec{A}, which is 12.0 m in a direction exactly 20∘20^\circ west of north. (This problem shows that A⃗+B⃗=B⃗+A⃗\vec{A} + \vec{B} = \vec{B} + \vec{A} .)
<b>Figure 3.56</b>
Figure 3.56
Question by OpenStax is licensed under CC BY 4.0
Final Answer

19.5 m, 4.66∘ S of W19.5 \textrm{ m, } 4.66^\circ \textrm{ S of W}

Note: While the final answer is correct, the video creates a bit of confusion about negative signs. The x-components should be negative, but the work was done using only magnitudes of the x-components, and used the drawing to figure out direction rather than signs. Please see the comments below for more details.

Solution video

OpenStax College Physics, Chapter 3, Problem 6 (Problems & Exercises)

OpenStax College Physics Answers, Chapter 3, Problem 6 video poster image.

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

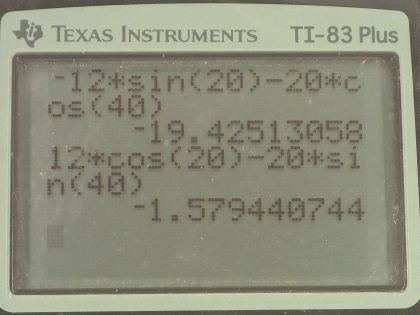
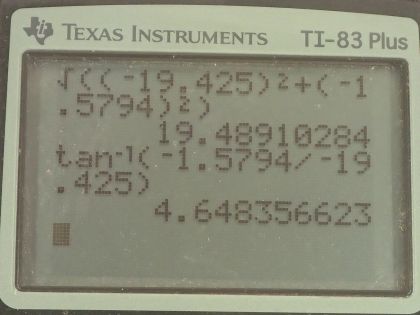
Calculator Screenshots

  • OpenStax College Physics, Chapter 3, Problem 6 (PE) calculator screenshot 1
  • OpenStax College Physics, Chapter 3, Problem 6 (PE) calculator screenshot 2
Video Transcript
This is College Physics Answers with Shaun Dychko. We're given this figure where somebody follows a path along vector A first and then along vector B second. Then this resultant is their displacement vectors connecting their starting point to their ending point. But we're told to instead consider moving along vector B first. That's starting along this vector at an angle of 40 degrees below horizontal. Then afterwards, do vector A and that's at an angle of 20 degrees in here with respect to the vertical and linked to 12 meters. Then figure out what this resultant will be and show that it's going to be the same resultant. We can kind of see that from the picture but we want to show that it doesn't matter what order you travel the paths in, you end up at the same ending point either way. We need to know what is the x-component of this resultant and that's going to be the x-component of vector A, which is this little portion here, plus the x-component of vector B, which is this portion here. This x-component of vector A is going to be the length of the hypotenuse A in this right triangle I'm showing in pink and that vector A has an angle of 20 degrees in here. This is being the opposite leg that we want to find for the x-component, we'll use the sine function to get that opposite leg multiplied by the hypotenuse. The hypotenuse length multiplied by sine of theta A is going to give us the x-component of the A vector. For the B vector, the x-component is on the adjacent leg of this triangle. We use cosine to get that. We have cosine of theta B is going to be multiplied by the length of B to get the x-component. That's 12 meters time sine 20 plus 20 meters times cos 40, which is 19.4 meters. That's the x-component of the resultant. The length from here all the way to here, that's Rx, it's 19.4 meters. Then we figure out the y-component of the resultant vector. We take the y-components of vectors A and B and add them together. For vector A, its y-component is positive because it's upwards. You can erase some of these highlights here so we can make some new highlights. We want to find what is this bit here. This is the y-component of vector A. That's going to be A multiply by cos of theta A because this is the adjacent leg of this triangle. That's 12 meters times cos 20 in that case. Then vector B, the y-component of this vector, and we're considering this triangle here now, there's y-component which is from the x-axis all the way down to the tip of vector B. That y-component is directed downwards and that's why it's negative. That's what the minus sign comes from. Thus we have minus 20 meters length times sine of 40 degrees because this is the opposite leg of this triangle compared to this angle theta B and use sine of it to find the components. That's negative 1.58 meters in total. The length of the resultant then is the sum of the squares of the components, square rooted. We have square root of 19.4 meters squared plus negative 1.58 meters squared, which works out to 19.5 meters. The direction of this resultant is going to be the inverse tangent of its y-component divided by its x-component. What we're finding now is this tiny angle here theta R. This is the angle we're finding now and it's this y-component, which is little tiny bit there. Then divided by the x-component, and we take the inverse tangent to find that angle. The inverse tangent of 1.58 meters divided by 19.4 meters, and I substituted in a positive number here because we already know what the direction of this angle is. I will say it's to the South compared to West to end up with 4.66 degrees. The final answer for the resultant is 19.5 meters, 4.66 degrees south of West.

Comments

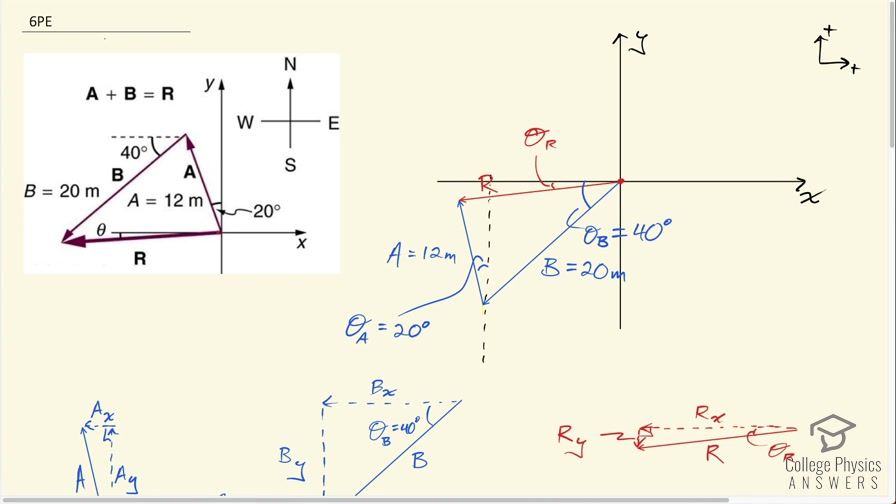
when finding Rx why is it not -12m for Ax? The arrow is pointing to the left.

Hi propiak,
Thank you very much for noticing this. You're quite right that AxA_x should be negative, and the same is true for BxB_x. It turns out to not affect the final answer since, when finding the magnitude of the resultant, we square the components of the resultant so the negative sign doesn't matter. Where is might have mattered is in finding the angle, but I ended up changing the sign of RyR_y from negative to a positive so that RyR_y divided by RxR_x was positive. This was justified by looking at the picture, and thinking only about the magnitudes of the components, then specifying direction at the end based on the picture. Looking at the drawing is what informed direction rather than using the signs to give direction. Admittedly, the signs were important for finding RyR_y since the y-components of AA and BB are in opposite directions and there needs to be subtraction to find RyR_y. I can see why this is confusing, and I'll flag this video for a re-do some day, but I hope with these comments that it makes enough sense in the mean time to help.
All the best,
Shaun