Question
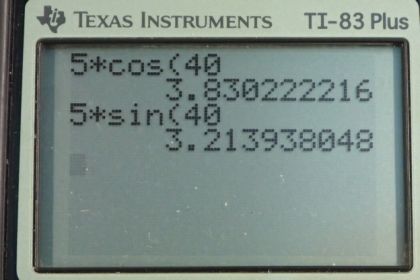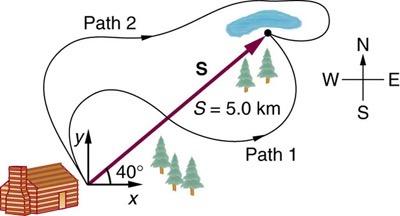
Find the north and east components of the displacement for the hikers shown in Figure 3.50.
<b>Figure 3.50:</b> The path of the hikers
Figure 3.50: The path of the hikers
Question by OpenStax is licensed under CC BY 4.0
Final Answer

East: 3.8 km3.8 \textrm{ km}

North: 3.2 km3.2 \textrm{ km}

Solution video

OpenStax College Physics, Chapter 3, Problem 3 (Problems & Exercises)

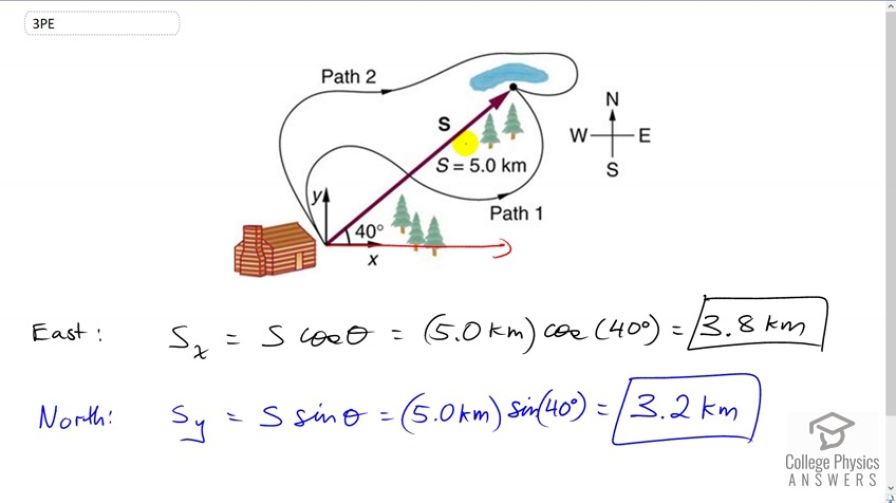
OpenStax College Physics, Chapter 3, Problem 3 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Select problem
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 3, Problem 3 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. The east component of the hiker's displacement is the horizontal component of this vector. We find that by taking the length of the vector of five kilometers, multiplying by cosine of this angle between the x component and the vector. So that's five kilometers times cos forty which makes 3.8 kilometers to the east. Then the vertical component is the amount by which they go upwards and this is the opposite leg of this triangle and so to find it, we multiply the hypotenuse which is the length of the displacement vector, by the sine of the angle to find the opposite component. That is the northerly component or the y component. So s subscript y equals s times sine theta which is five kilometers times sine forty which makes 3.2 kilometers to the north.

Comments

Wouldnt we use cos for north since it covers adjacent and hypotenuse? Can you explain the logic behind knowing when to use sin or cos

you are talking about SOH CAH TOA right now which deals with sides. We only have one side and one angle, that angle is not 45 degrees so y and x aren't the same which means we will need to use sin and cos. If you want to understand this you should take trigonometry unit circle on khan academy. sin and cos are just a way of determining what coordinates in a circle does a line represent. In this case the line is 5 units and the angle is 40. In a unit circle( 1 unit radius) sin(90) = 1, sin(270) = -1, cos(0 or 360) = 1, cos(180) = -1 . It's really just a coordinate plane. So if the radius is 5 then 5cos(0) for example is equal to 5. If you still don't get it I highly suggest you take a trig coarse you only need algebra 2 to understand it.