Question
Derive for the range of a projectile on level ground by finding the time at which becomes zero and substituting this value of into the expression for , noting that .
Final Answer
see the solution video for the derivation
Solution video
OpenStax College Physics, Chapter 3, Problem 49 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
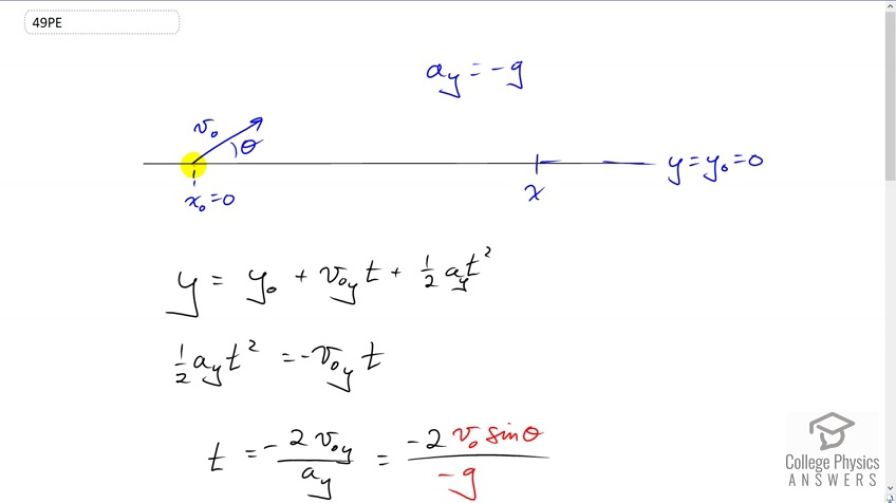
This is College Physics Answers with Shaun Dychko. We are going to derive the range formula. Now the range formula assumes that the projectile lands at the same height that it started with and so we’ll say that the final height y equals initial height y naught. It’s going to travel to some horizontal position x starting at some horizontal position x naught and the acceleration will be negative g. It’s gonna have a launch angle of theta and initial speed of v naught and the technique we’re recommended is first find out the time in the air, and then substitute that into our formula for the horizontal position. And then solve for the range, which is the difference between the final and initial horizontal positions. So the vertical position is the initial vertical position plus the initial vertical component of velocity times the time in the air, plus one half times vertical acceleration times time squared. And y naught and y, we’ll take to be zero. We don’t have to make them zero, they just have to be the same and we could have subtracted y naught from both sides and then said well since y equals y naught, that means y minus y naught equals zero. Either way, these terms disappear. And then we’ll take this term to the other side by subtracting v naught y tfrom both sides and switch the sides around so that we have the t squared term on the left. We’ll multiply both sides by two and divide both sides by ay t and the ts cancel on the right, and we have t to the power of one on the left. Well everything else disappears on the left and t is isolated. On the right hand side we have negative two times the initial vertical component of velocity divided by vertical acceleration. Now this v naught y is v naught times sin theta because it is the opposite leg of this triangle here, and so we use sine of this angle multiply by length of the hypotenuse to get v naught y. We are dividing by the acceleration which is negative g. Cancelling the negatives, we get the time in the air is two times the initial speed times sin theta divided by g. Then, we consider the horizontal direction. That is x equals x naught, the final horizontal position equals initial horizontal position plus the initial horizontal component of velocity times time. I’ve made a substitution for v naught x as v naught cos theta because v naught x is the adjacent leg of this triangle. And so we use cosine of the angle multiply by the hypotenuse in order to get the adjacent leg. I replaced x minus x naught with a capital R because this is the range, the difference in the x positions. So then we take equation one for t and replaced t in this equation, let’s call it equation two here. So I repeated equation two, R equals v naught cos theta, but I replaced the t with two v naught sin theta over g. And then multiply through here, you get v naught times v naught makes v naught squared, multiply by bracket two times sin theta times cos theta. And you know when you’re multiplying different factors together, you can multiply them in any order and I chose to group them like this because two sin theta cos theta is a trigonometric identity for sin two theta. So we can replace this bracket with sin two theta and that’s what I’ve done in the final line, and so we have derived the range formula. It is initial speed squared times sine of two times the launch angle divided by g.