Solution video
OpenStax College Physics, Chapter 3, Problem 10 (Problems & Exercises)
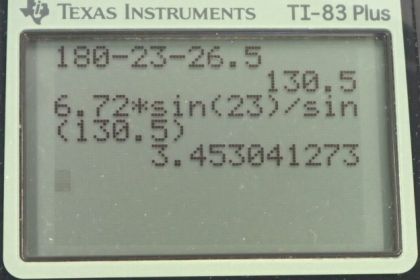
Calculator Screenshots
Comments
Could you help me find which part of chapter 3 this formula is found? Thanks!
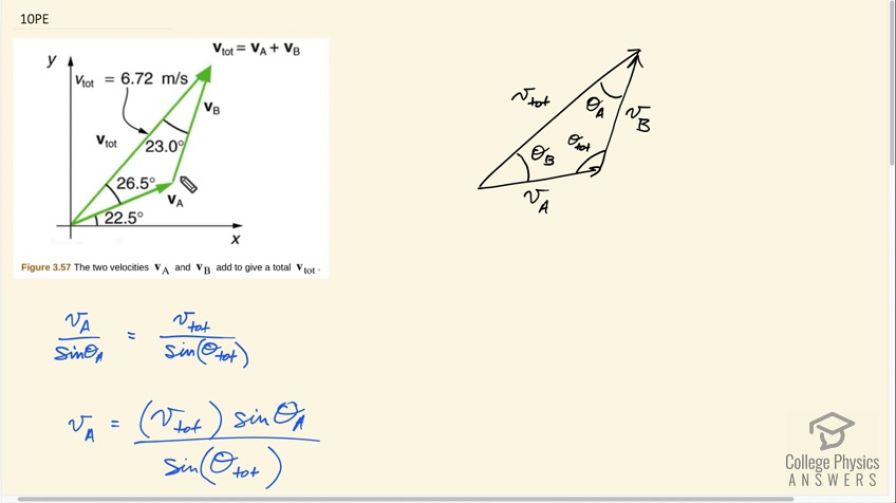
Thanks for the question. This actually isn't in the textbook I don't think. It's a technique for solving triangles that I was hoping students would see in their math classes. It's the Sine Law: https://www.mathsisfun.com/algebra/trig-sine-law.html. It's super useful, and can be used to solve any triangle.
All the best,
Shaun
I just got this problem wrong on my assignment when I used your answers
Hi rickylove, the answer here is correct so far as I can tell but if there's a point in the video where you think there's an error, please mention the time when you think that is. Using the sine law might be an unfamiliar problem solving approach. Each student needs to choose the method that works for them.
All the best,
Shaun
Hi Shaun,
Can we solve for Vb once Va is discover by just subtracting Va from V total. If so shouldn't the answer for the equation be Vb = 3.27? Thank you in advance.
I just want to mention that this worked for my problems when I used this method. So it does seem to be correct as far as I can tell here.
Is there an alternate way to solve this without the sine law?
Hi torihall,
Thank you for the question. Yes, it's possible to solve this without the sine law. One alternative approach would be to use components: create an equation for each axis, where the x-component of the resultant equals the sum of the x-component of vectors A and B, and likewise for the y-axis. You would need to calculate the angle of vector B with respect to the horizontal first, based on the information in the picture. This creates two simultaneous equations which can be solved, probably by the method of substitution where you solve one of them for vector A in terms of vector B and v_tot, and substitute that into the other equation. The algebra gets a bit messy, so my preference is for the sine law approach, but the component method is good practice too.
I know this is a bit abstract, but hopefully it can help you start your own solution with this method,
Shaun
Hi, thanks for these videos, I was just wondering if you could explain why you used the angle of 23 degrees for angle A. how do you determine which angles are which. Im just a bit confused by that. Thanks !
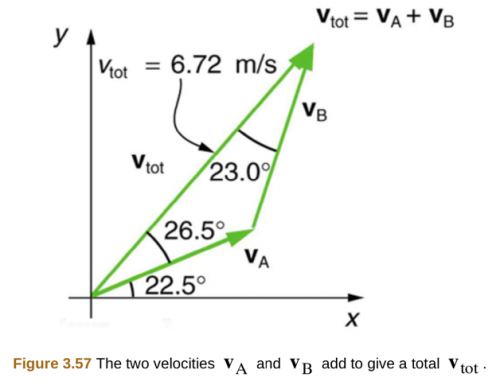
Hello, are you asking why each angle gets labeled with their particular letters? Angle A is the corner opposite the side labeled with "A". Opposite means, with your pencil on a side (such as ), if you move your pencil through the triangle to the corner that is not at either end of the side, that's the opposite angle.
Hope this helps,
Shaun
I see that the sine law is the one that works best, but could you explain how you determined the sine law is the one you should use for this problem? thanks!
Using the sine law is just personal preference. To me, it's less effort than to use components. The component method in this case would mean creating two simultaneous equations, one for each dimension, then solving for the two unknowns and ...
If Vtot = 6.72 why Va+Vb does not add up?
Hi Dieter, thank you for the question. Since and form two sides of a triangle with , we expect the numerical lengths of and to have a total that is greater than the length of . The shortest distance between two points, which in this case is the origin and the top of or , is a single straight line connecting them. is that single shortest straight line. The alternative path along first , then will be longer.
Hope this helps,
Shaun