Question
(a) Use the distance and velocity data in Figure 3.62 to find the rate of expansion as a function of distance.
(b) If you extrapolate back in time, how long ago would all of the galaxies have been at approximately the same position? The two parts of this problem give you some idea of how the Hubble constant for universal expansion and the time back to the Big Bang are determined, respectively.

Final Answer
- The recession velocity is directly proportional to distance from the Milky Way Galaxy. The constant of proportionality, called the Hubble Constant, is on average
- 20 billion years.
Solution video
OpenStax College Physics, Chapter 3, Problem 64 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
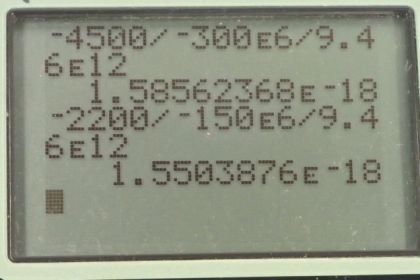
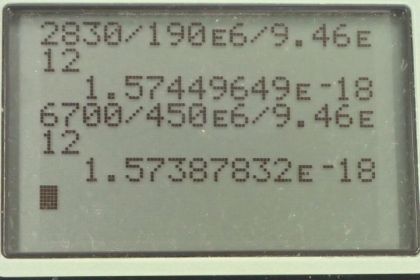
This is College Physics Answers with Shaun Dychko. This question ask us to find the velocity with which the galaxies are receding from us. We’re in the Milky Way galaxy number three here. We’re meant to find this recession velocity of the other galaxies as a function of distance. And so we'll take the recession velocity that we're given, and we'll divide it by the distance the galaxy is from us. And this quotient has a name, it's called Hubble's Constant. And they talk about it in chapter 34, this is equation number one. And we're gonna find that the ratio of recession velocity over distance from us is the same essentially for all the different galaxies. So for galaxy number one, it's receding from us at 4500 kilometers per second. And it's 300 mega light years away. So we divide those numbers and then convert it into units of reciprocal seconds, by multiplying by one light year for every 9.46 times ten to the 12 kilometers. And you can look up this number in Google, and you get 1.59 times ten to the minus 18 reciprocal seconds. Which could also be written s to the negative one. So yes, because the light years canceled and the kilometers cancel leaving us with per seconds. And we do that for galaxy two; it's receding at 2200 kilometers per second. And it's 150 mega light years away. This works up to 1.55 times ten to the minus 18. Galaxy four is receding at 2830 kilometers per second and it’s 190 mega light years away. So we take the ratio of those numbers and this works out to 1.57 times ten to the minus 18 reciprocal seconds. And then galaxy five is 6700 kilometers per second and is 450 mega light years away. And that works out to 1.57 times ten to the minus 18 reciprocal seconds. So there's this, basically there’s a constant of proportionality relating the recession velocity to the distance. And if you were to plot it on a graph, it would be a straight line. We can take an average of this, this would be the slope of that line. If you wanted to have v as a function of distance and that slope will be Hubble’s Constant if you rearrange this. And we take the average of all those values we found here and we get 1.57 times ten to the minus 18 reciprocal seconds. So the recession velocity is directly proportional to the distance. Then we're ask to figure out what age of the universe does this value suggest. Well, this value for h Hubble's Constant is the recession speed, divided by distance. And this is the same as one over time. And we can then solve for time by multiplying this by t over h average. Then multiply this side by t over h average. And we end up with time is one over the average Hubble's Constant. So that works out to 6.37 times ten to the positive 17 seconds. Which we convert into billions of years by multiplying by one hour for every 3600 seconds. And then by one day for every 24 hours, then by one year for every 365 days. And then one billion years for every ten to the nine years. And we get 20 billion years. Is the suggested age of the universe. Whereas if you look it up on Google in fact, it's about 13 or so.