Solution video
OpenStax College Physics, Chapter 3, Problem 11 (Problems & Exercises)
Calculator Screenshots
Comments
I don't think this answer is right
Do you see any specific error? So far it looks fine to me, but do let me know if you notice something specific.
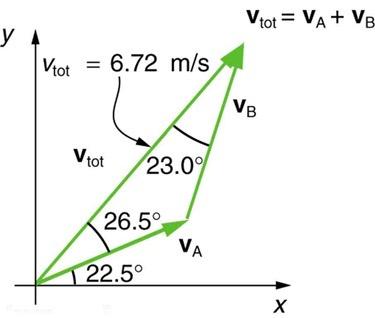
how do you know to use 49 degrees for both the x and y components? why not the 23 degrees?
When finding components we want to imagine a right triangle (a triangle with a angle, in other words) that has the vector as it's hypotenuse (which is the name of the longest side opposite the angle), and the components are the legs. When the legs of the right triangle are parallel to the x and y axes, we call these legs x and y components along these axes. All this is to say that the angle is the angle in the imaginary right triangle with legs parallel to the x and y axes. It's the angle between the vector and the x-axis. Using would find components along different axes.
How can you use this to find the magnitudes of velocities for vector A and vector B?
Knowing the components of the resultant isn't actually useful for finding the magnitudes of vectors A nor B. This is because vectors A and B could have a variety of different lengths, but with adjusted angles, they could nevertheless create the same resultant.
Nevertheless, since so many angles are given in the problem, you can figure out vector A and B magnitudes, you just can't do it with the resultant components. I would figure out the third angle inside the vector triangle (the three are supplementary), then use the sine law to find the lengths of vectors A and B.
I'm not coming up with the same answer when putting the equation in?
Keep in mind that we're finding the components of the resultant vector (it's a bit confusing that the picture has three vectors on it, so let's be sure we're looking at the right one. It's labeled ). Have you looked at the calculator screenshot showing how I plugged this into the calculator? Are you seeing anything different on your calculator, or something amiss with how I've plugged values into mine?
Hey check this out. So I'm following along your video instructions and the calculator screenshot-- i'm plugging in my assignment numbers (vtot=6.44 and o=23.5- instead of 6.72 and 22.5)
Consistently, I was coming up with the wrong answer. So then I checked your calculations... and google calculator gave me a different calculation of 6.72*cos(49) = 2.01998189396
Turns out... your calculator is right, and the scientific calculator online that i was using, was not accurate! This is the link. I wish I could show you a screenshot. I ended up using a different calculator, and it came out the same as yours.
https://www.google.com/search?q=scientific+calcultor&rlz=1C1RAEH_enUS88…
I learned today from my prof. that the scientific calculator can give you wrong answers when in the wrong mode. If you are using Casio make sure to look at the top and you should see a D, which stands for degrees. I did not have it on and it gave me the wrong answers.
You're quite right GabiFerreira, and thank you for responding to the other student's comment. Calculators need to be told whether the angles you're entering are in degrees (for which you want the "D" you mentioned), or whether the angles are in radians.
How would you find the angle thats 22.5 if you werent given it?



