Question
(a) What resistance would you put in parallel with a
galvanometer having a sensitivity to allow it to be used as an ammeter that has a full-scale deflection for ? (b) What is unreasonable about this result? (c)
Which assumptions are responsible?
Final Answer
- A negative resistance is nonsensical.
- It isn't possible to have a full scale deflection with a current less than the sensitivity of the galvanometer.
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 56 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
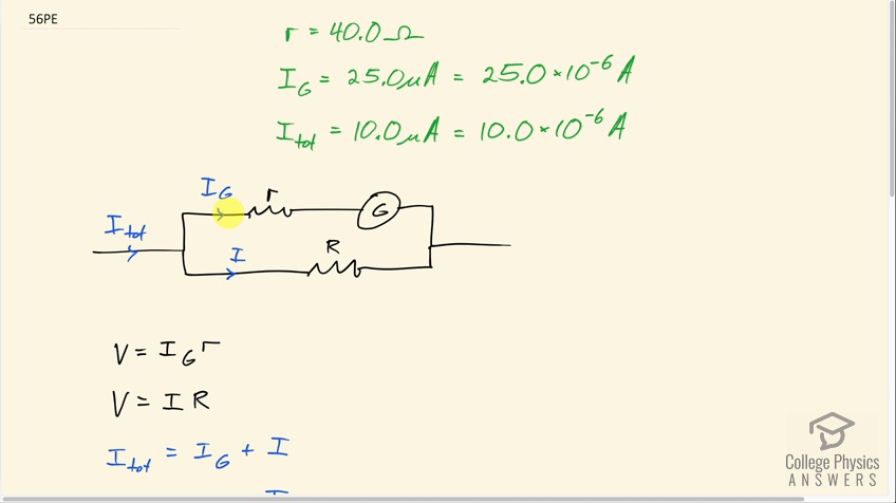
This is College Physics Answers with Shaun Dychko. So we imagine that we have a galvanometer that has a sensitivity of 25.0 microamps which is to say that when the current is 25.0 microamps through this galvanometer, it has a full scale deflection and its internal resistance is 40 ohms and the total current being measured here is 10.0 microamps and that's supposed to give a full scale deflection which already we can tell is a contradiction of terms because you know, full scale deflection occurs at 25.0 microamps so how is it possible to happen at 10.0 but anyway... we'll see what the problem is later. So this galvanometer is put in parallel with a shunt resistance and we have to figure out what should this shunt resistance be such that we can make all this work out? So the voltage between these two parallel branches is the same so V with no subscript on it because this is the same V. On the one hand, it's the current through the galvanometer multiplied by the resistance of the galvanometer; on the other hand, it's this current through the bottom branch multiplied by this shunt resistance R. Now the total current going into this junction equals the galvanometer current plus the current through the shunt resistance— that's Kirchhoff's junction rule— and we can solve this for I by subtracting current through the galvanometer from both sides and then switching the sides around. So this current I is I total minus I galvanometer, which we can then write in place of I in this formula here. So this is the voltage through the bottom branch and it equals the voltage through the top branch and we can solve for R by dividing both sides by I total minus I G. So the shunt resistance then is 25.0 microamps times 40.0 ohms divided by 10.0 microamps minus 25.0 microamps which is negative 66.7 ohms; that's what the math tells us but we know that the physics doesn't work out because a negative resistance is non-sensical. So it isn't possible to have a full scale deflection at 10.0 microamps because that's less than the sensitivity of the galvanometer.
