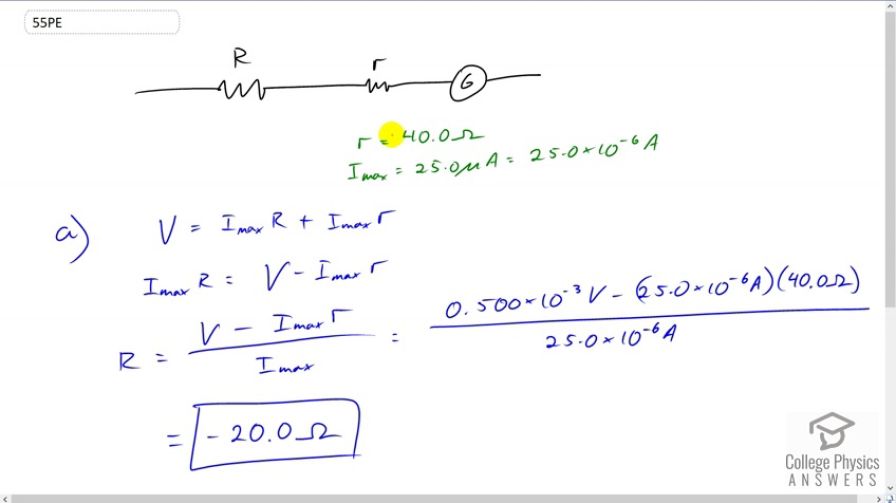
Suppose you have a $40.0\Omega$ galvanometer with a $25.0\mu \text{A}$ sensitivity. (a) What resistance would you put in series with it to allow it to be used as a voltmeter that has a full-scale deflection for 0.500 mV? (b) What is unreasonable about this result? (c) Which assumptions are responsible?

Video Transcript

This is College Physics Answers with Shaun Dychko. We have a galvanometer with a sensitivity of 25 microamps so full scale deflection occurs when that current goes through it, and it has an internal resistance of 40 ohms. So the question is what resistance should be put in series with it to allow it to be used as a voltmeter with a full scale deflection of 0.5 millivolts? Well if it's a voltmeter we're going to have the voltage between this point and this point and that's going to equal the full scale current flowing through it multiplied by this R that we're trying to find, plus the current multiplied by this internal resistance of the galvanometer. We can put this term by itself on one side by subtracting I max times little r from both sides. We get I max times the extra resistance capital R, equals V minus I max times internal resistance R. Then divide both sides by the current. So R is the voltage at which full scale deflection is meant to occur, minus the sensitivity times the internal resistance divided by the sensitivity. So we have 0.5 times ten to the minus three volts, minus 25 microamps times 40 ohms, divided by 25 microamps which gives negative 20 ohms. Now that answer is not realistic because resistance can't be negative. So the voltage must in fact be more than 0.5 millivolts. This galvanometer cannot be used to have a full scale deflection at this voltage.