OpenStax College Physics for AP® Courses, Chapter 21, Problem 6 (Problems & Exercises)

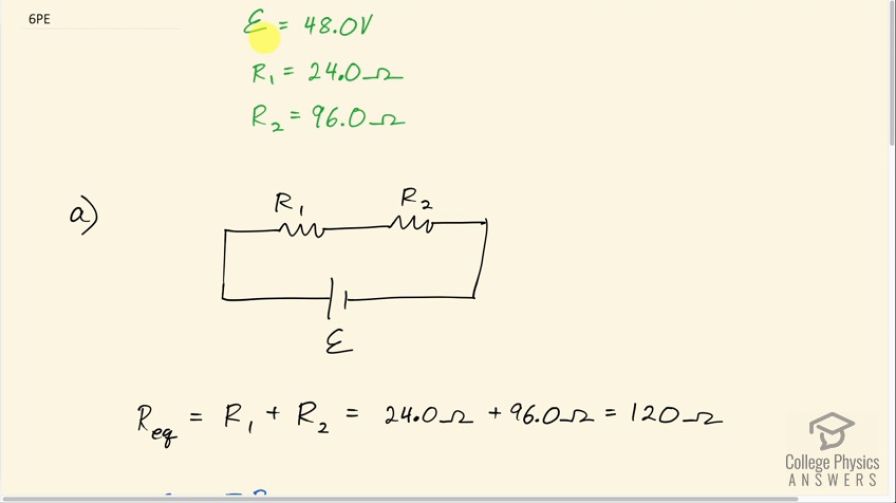
This is College Physics Answers with Shaun Dychko. We have a 48.0 volt battery and voltage for a battery is traditionally written with this scripted ε for emf; we have a resistor—resistor one we will call it—is 24.0 ohms and resistor two is 96.0 ohms and part (a) says put these resistors in series and then figure out the current and power through each resistor. So to find the current, we need to figure out what is the equivalent resistance of these two resistors so we have to imagine a circuit with only a single resistor— R eq for 'equivalent'— and what resistance would this need to be to have the same resistance as these two separate resistors in series and once we know that, we can figure out what the current is in this circuit which will be the same as the current in this circuit. So the equivalent resistance for resistors in series is the regular sum of the resistances. So that's 24.0 ohms plus 96.0 ohms to make 120 ohms. Now the Ohm's law which says voltage is current times resistance can be rearranged to solve for I by dividing both sides by the equivalent resistance and so then the current then is the emf divided by the equivalent resistance so that's 48.0 volts divided by 120 ohms which is 0.400 amps and that's gonna be the same as the current through resistor one and the current through resistor two because when they are in series like this, the current through each circuit element will be the same. So the power dissipated by resistor one is going to be the current through it squared multiplied by resistor one. So that's 0.400 amps times itself times 24.0 ohms which makes 3.84 watts and for resistor two, the power dissipated will be 0.400 amps squared times 96.0 ohms which is 15.4 watts. Now in part (b), we are asked to answer the same questions about the power dissipated in each of the resistors and the current through each resistor when they are connected in parallel and so here's a drawing of that. And so each resistor will experience the full voltage of the battery and I am sort of using the letter V and the scripted ε interchangeably here—I hope that's not too confusing—but this is Ohm's law here which says V equals IR and we can divide both sides by R to solve for V and then we have the current one then is going to be this emf divided by resistor one. So that's 48.0 volts divided by 24.0 ohms, which is 2.00 amps and the current through the second resistor is that same emf—48.0 volts—divided by resistor two, which is 96.0 ohms, and this makes 0.500 amps. And the power dissipated by the first resistor will be the voltage across it squared divided by its resistance so that's 48.0 volts squared divided by 24.0 ohms, which is 96.0 watts and the power dissipated by resistor two will be the same 48.0 volts squared divided by 96.0 ohms, which is 24.0 watts.