Question
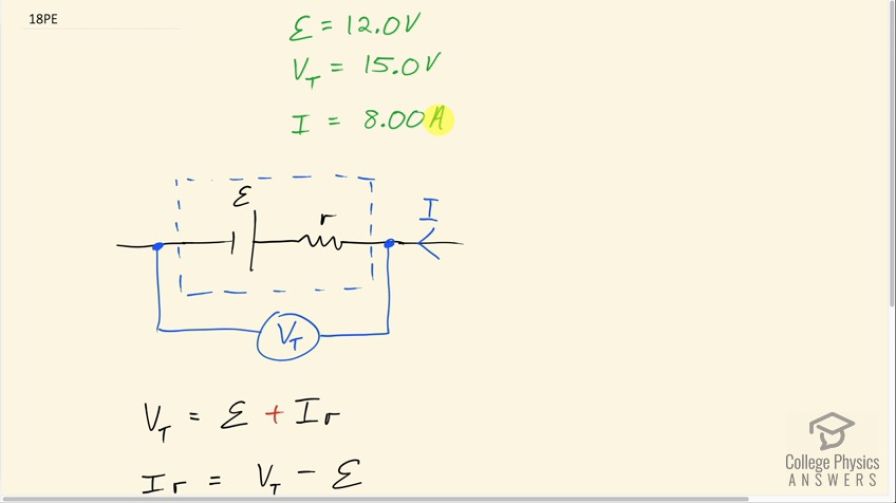
What is the internal resistance of an automobile battery that has an emf of 12.0 V and a terminal voltage of 15.0 V while a current of 8.00 A is charging it?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 18 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A battery with an emf of 12.0 volts is being charged by a current of 8.00 amps and while that's happening, the terminal voltage of a battery is 15.0 volts and the question is figure out what is the internal resistance of the battery? Now it might be a little bit surprising to see this terminal voltage being greater than the emf because our usual formula for terminal voltage is emf minus the current multiplied by the internal resistance in which case the terminal voltage is always less than the emf. But that formula needs to be adjusted because what's different about this question is that the battery is being charged and so the current is going from right to left... the current is going this way through the battery which is what happens when it's being charged. And so if you consider Kirchhoff's loop rule, when we are going across an emf from negative to positive that means we add that emf and when we go across a resistor, if we are traversing in this direction— which we want to do since for a battery, we typically start at the negative and then move to the positive end; this short one is the negative and the long one is positive— when we move across a resistor in the opposite direction to the current going through it then that potential difference is positive so it's going to be positive I times r and this is what's happening when charging is occuring is that the current is going through this resistance in the opposite direction to what we are used to in a typical circuit where the battery is providing the current. Okay! So we have traversed this internal resistance from left to right, which is the opposite direction to the current going through the battery and for that reason, we have a positive potential difference here. So our terminal voltage then is going to be the emf plus the current multiplied by the internal resistance. So we'll subtract emf from both sides and then move this Ir to the left or switch the sides around, in other words, and so Ir equals V T minus ε and then divide both sides by I to solve for the internal resistance r. So that's 15.0 volts minus 12.0 volts divided by 8.00 amps, which is 0.375 ohms.
