Question
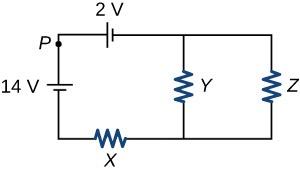
Figure 21.59 The figure above shows a circuit containing two batteries and three identical resistors with resistance R. Which of the following changes to the circuit will result in an increase in the current at point P? Select two answers.
a. Reversing the connections to the 14 V battery.
b. Removing the 2 V battery and connecting the wires to
close the left loop.
c. Rearranging the resistors so all three are in series.
d. Removing the branch containing resistor Z.
Final Answer
(a) and (b)
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 1 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Video Transcript
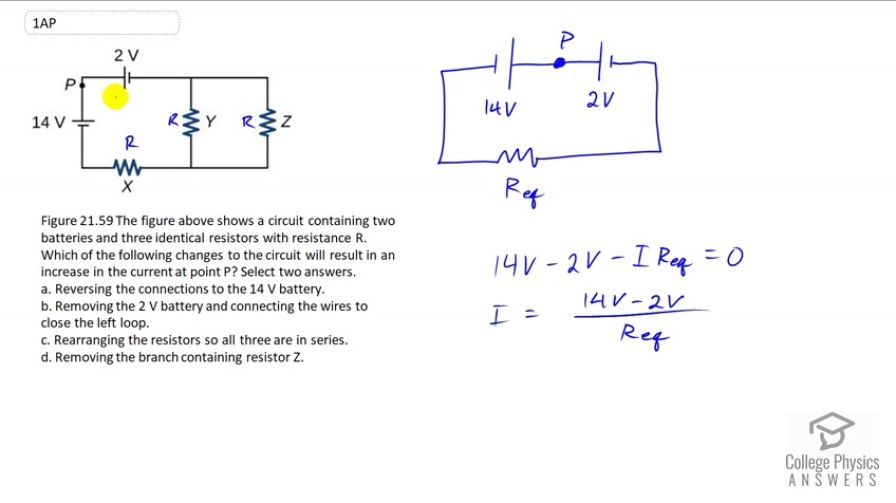
This is College Physics Answers with Shaun Dychko. In this circuit diagram, we have three resistors, all as the same resistance R. And we have an EMF of 14 Volts and another EMF of two Volts. And this point P as our point of interest. We want to increase the current through this point by doing two of these four things. And we have to select which two things result at an increase at the current there. So, I’ve redrawn the circuit here with all three resistors replaced by one equivalent resistance whatever it is. We have these two added in parallel and sum could be added in series with this one. But we really don’t need to add them all up. Let’s just say that there is some equivalent resistance. Now, notice how the polarities of these EMFs are opposing here. We have the positive play to the 14 Volt EMF connected to the positive end of the two Volt EMF. So, if we were to do the loop rule on this equation to analyze it to find the current in it. Let’s traverse loop on this direction. Suppose that the current is also going that direction. Now, if we start here, we would traverse from the negative to the positive end of this EMF. And that would be a positive 14 Volts. But then going from this positive end to this negative terminal of this EMF, that means we do have minus there because that’s a drop in EMF when you traverse in EMF from the positive to the negative. So it’s minus two Volts. And then traversing this equivalent resistance as the same direction as the current through it is minus current times Req equals zero. And we could solve this for I by moving this term to the right side. That makes it positive and then divide both sides by Req. And we get I is equals 14 minus two over Req. So, now that we have an expression for current. This is the current through every point including the point P. Now we can fiddle with things here to see how it will change this expression. If we were to reverse the connection to the 14 Volt battery and make the 14 Volt battery like this, instead. Then, that would make this term become a negative. Like if you started here, ‘coz you will be traversing from the positive to the negative end. And this will be a negative there. And then the current will be negative 16 Volts over Req instead of positive 12 over Req. And the negative versus positive doesn’t matter. It only affects the direction. It’s the magnitude of the current that’s important here. And having negative 16 over Req is a larger magnitude thatn 12 over Req that we start with. And so yes, doing that would increase the magnitude of the current through point P. And if you were to remove this EMF and just connect this wire directly here, would that increase the current? And the answer again is yes, because you’d be removing this term here basically. So we’d have 14 Volts minus nothing over Req, which in 14 Req will be more than 12 over Req. So, b also works. So that finishes the question but we can just exclude c and d just to be sure. If you put all the resistors in series, it’s going to increase their equivalent resistance instead of reduce the current. And if you remove this branch here, then you’re again increasing resistance because you’ve taken away one of the options for the current when it gets to this junction that it has two ways that it can go. And that collection of options reduces the equivalent resistance. So the more resistors you have in parallel, the lower the equivalent resistance of that collection is. And that by removing resistors head, you’d be limiting this current to only one option and that’s increasing the resistance between this junction and that junction. So that would also reduce the current. So a and b are the answers.