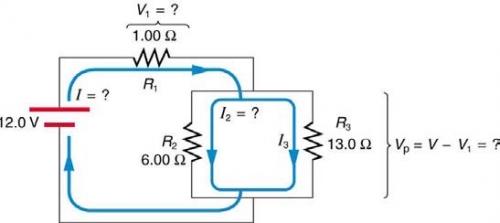
Question
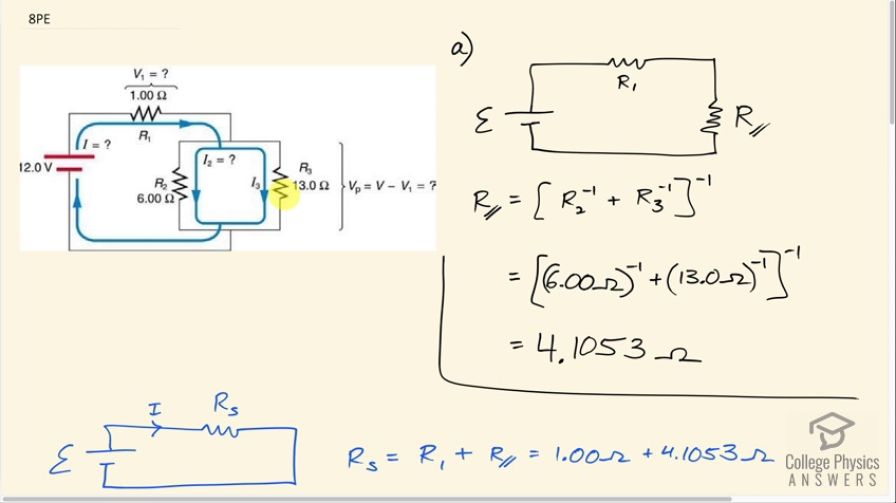
Referring to Figure 21.6: (a) Calculate (b) Find the total power supplied by the source and compare it with the sum of the powers dissipated by the resistors.
Final Answer
- . The total power dissipated equals the sum of the powers dissipated in each resistors, as expected due to conservation of energy.
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 8 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
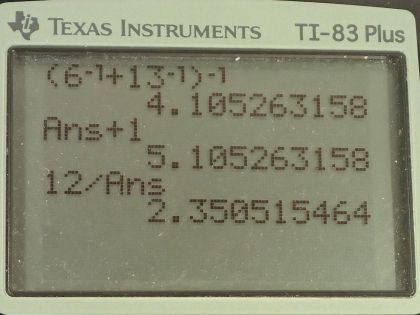
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In part (a) of this question, we are asked what is the power dissipated in resistor three in this circuit? So this circuit consists of a 12.0 volt power supply providing this current that goes first through this resistor R 1 and then it goes in parallel through resistors two and three. So to answer what is the power dissipated in resistor 3, we need to know what is the voltage across it or in other words, what is the voltage across this parallel part of the circuit and then we'll take that voltage squared divided by the resistance to figure out the power dissipated in the resistor. But to figure out the voltage across this parallel part, we need to first find the voltage drop across this resistor R 1 because then that we will subtract from 12.0 volts to figure out the voltage across the resistor three. Okay! So the first step is figuring out the voltage drop across R 1. So to do that, we will rewrite this circuit with this picture here where I have replaced these parallel two resistors with a single equivalent resistance which will be the reciprocal of the sum of the reciprocals of each of the resistors. Often you see this formula written with fractions—and that's fine— I prefer to write it as with exponents negative 1 because that's what I am gonna be plugging into my calculator; it's less button pushing than writing... or than typing 1 divided by such and such but just in case you want to see the other way, it would be 1 over R 2 plus 1 over R 3 and then the left side would be 1 over R parallel equals 1 over R parallel but let's do a little bit of this reciprocal with exponent negative 1 here because anything to the exponent negative 1 is 1 over itself so this is the special exponent that does reciprocal. So we can take all of this to the power of negative 1 and that gives the reciprocal of this everything in the brackets and then that is R parallel. Okay! So we have 6.00 ohms is resistor two and we take its reciprocal and then add to that 13.0 ohms with its reciprocal and then add them together and then that result gets to the power of negative 1 and you end up with 4.1053 ohms and so that's R parallel. And then we need to combine these two resistances to get one final equivalent resistance for the entire circuit— we will call it R s for series here because this result is in series with this R 1— and we add them together directly when resistors are in series so we have 1.00 ohm plus this 4.1053 ohms and that's 5.1053 ohms. Now we can use Ohm's law and say that the voltage across this resistor equals the current through it multiplied by its resistance and we want to know the current because that would be the current through R 1 and then we can find the voltage V 1 by multiplying this current by R 1. Okay! So first finding the total current from the battery, we divide both sides by R s to solve for I and so the current then is 12.0 volts— provided by the battery— divided by the total equivalent resistance of the entire circuit and that works out to 2.3505 amps. So now the voltage across resistor one, which is one of the reasons why we did all this work is to find this voltage is the current through it which will be the same as the current drawn from the battery— as we figured out here— multiplied by resistance one. So that's 2.3505 amps times 1.00 ohm which is 2.3505 volts. And here's a more formal way of saying why we can subtract this number from 12.0 to get the voltage across from R 3: we are gonna use Kirchhoff's loop rule, which says that considering any loop, the total voltage gains and drops have to add to zero so this is gonna be our loop that we think about here and we are gonna traverse it in this direction and as we go from the negative terminal to the positive terminal of the battery that's a gain in potential and so that's why this emf has a positive in front of it. And then we will be traversing this resistor in the same direction as the current through it so that's gonna be a voltage drop so we have minus I times R 1 and then... well, which is V 1 and then minus V 3 equals zero and we want to find V 3 so let's add V 3 to both sides and then switch the sides around and we get V 3 equals ε minus V 1. So we have 12.0 volts minus 2.3505 volts which is 9.6495 volts. There! That is the number that we square and divide by resistance three, which is 13.0 ohms, to figure out what is the power dissipated by resistor three? Then that is 7.16 watts. So part (b) says compare the total power dissipated in the entire circuit with the sum of the powers dissipated in each of the component resistors and conservation of energy tells us that we should get the same answer but we are gonna verify that we do. So the total power dissipated is going to be the current squared multiplied by the total equivalent resistance, which I call R s up here, and so that is 2.3505 amps squared times 5.1053 ohms and that's 28.2 watts. Now let's find the resistances of each of the resistors. So resistor one dissipates a power of the current squared and that is the total current coming from the battery goes through resistor one, we square that, multiply it by 1.00 ohm and we get 5.5249 watts. Resistor two dissipates a power equal to V 2 squared divided by R 2 but V 2 is the same as V 3 because these resistors are in parallel— the voltage across them is the same— and so we have 9.6495 volts squared divided by 6.00 ohms, which is 15.5188 watts. So we add this number and this number to the power in resistor three that we found before and we find that they all total 28.2 watts and so that's good because that's supposed to be the same; we expected that due to conservation of energy. So the total power dissipated from the battery, which we found here, equals the sum of the powers dissipated in each of the resistors.