Question
A and a capacitor can be connected in series or parallel, as can a and a resistor. Calculate the four RC time constants possible from connecting the resulting capacitance and resistance in series.
Final Answer
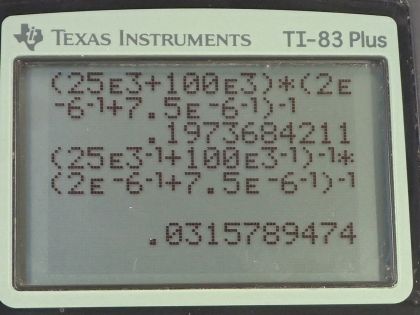
Both in series: 0.197s
Resistors in parallel, capacitors in series:
Resistors in series, capacitors in parallel: 1.19s
Both in parallel: 0.190s
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 66 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have two capacitors and two resistors and we are gonna connect them in the capacitors in series and parallel and we will connect the resistors in series and parallel and put those two combinations together such that we have four different ways of arranging these circuit elements and each of those arrangements will have different time constants. So the first capacitor is 2.00 microfarads and the second one is 7.50 microfarads; the first resistor is 25.0 kiloohms and the second one is 100 kiloohms and I have written all those with their instead of prefixes with their times 10 to the whatever they need and in the first circuit, we will have resistors in series and capacitors in series and so the time constant will be the total resistance multiplied by the total capacitance. So for resistors in series, we add them directly the total resistance will be R 1 plus R 2; for capacitors in series, we add them the same way that we do resistors in parallel we take the reciprocal of each capacitance, add together those reciprocals and then take the reciprocal of that sum. This might also be written as C s equals 1 over C 1 plus 1 over C 2 all to the power of negative one you might have seen it written that way or you might see 1 over C s equals 1 over C 1 plus 1 over C 2 all of these are the same, just written differently I prefer to write it like this because this is how I punch it into my calculator I go bracket first capacitance and then there's a negative one exponent button plus the second capacitance negative one exponent button close bracket negative one exponent on that whole thing and that gives us our answer for the capacitance in series. Alrighty! So we have 25.0 kiloohms plus a 100 kiloohms multiplied by 2.00 microfarads to the negative one plus 7.50 microfarads to the negative one all to the negative one giving us 0.197 seconds is the time constant with everything in series. Then we have resistors in parallel and the capacitors in series and so this is the formula for adding resistances in parallel and it's analogous to adding capacitors in series. So we have 25.0 kiloohms to the negative one plus a 100 kiloohms to the negative one all to the negative one and then multiply that result by two microfarads to the negative one plus 7.50 microfarads to the negative one all to the negative one giving us 3.16 times 10 to the minus 2 seconds is the time constant with resistors in parallel and capacitors in series. Then we have the resistors in series but the capacitors in parallel and when capacitors are in parallel, they add directly. So in this case, the time constant will be 25 kiloohms plus 100 kiloohms times 2.00 microfarads plus 7.50 microfarads and this works out to 1.19 seconds. Then we have resistors in parallel and capacitors in parallel so resistors in parallel add this way R 1 to the negative one plus R 2 to the negative one all to the negative one and then capacitors in parallel just add the capacitances together, C 1 plus C 2. So we have 25 kiloohms to the negative one plus 100 kiloohms to the negative one all to the negative one times 2.00 times 10 to the minus 6 farads plus 7.50 times 10 to the minus 6 farads giving us 0.190 seconds for the time constant in this case with everything in parallel.