Question
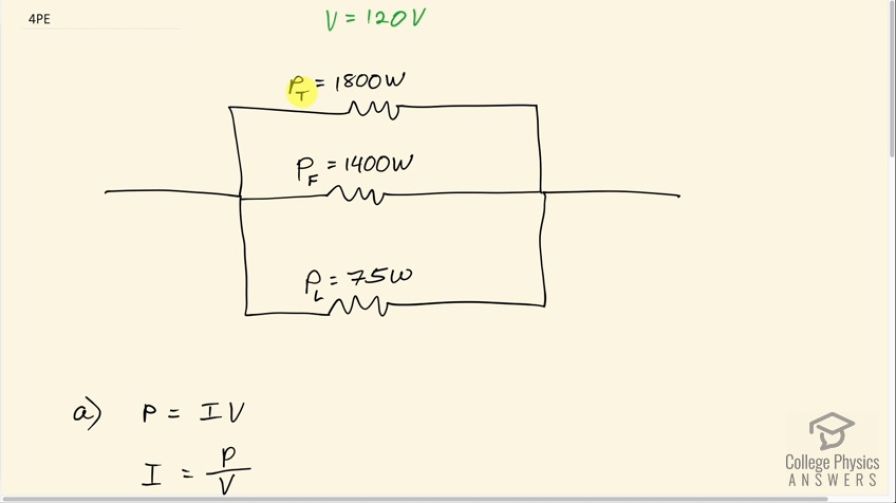
An 1800-W toaster, a 1400-W electric frying pan, and a 75-W lamp are plugged into the same outlet in a 15-A, 120-V circuit. (The three devices are in parallel when plugged into the same socket.). (a) What current is drawn by each device? (b) Will this combination blow the 15-A fuse?
Final Answer
- , ,
- , therefore yes, the combination will blow the 15 amp fuse.
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 4 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have three appliances connected in parallel to a 120 volt outlet and the first appliance is a toaster drawing 1800 watts and we have a frying pan drawing 1400 watts and a lamp drawing 75 watts and the question is what is the current going through each device assuming that the fuse hasn't blown yet? So in part (a), we can see that power is current times voltage and we can solve for the current I by dividing both sides by V so the current then is power divided by voltage. And so we take each power for each device and divide them by 120 volts because they all experience the same voltage since they are connected in parallel to this regular North American outlet. So for the toaster we have 1800 watts divided by 120 volts that is 15 amps; the frying pan is 1400 watts divided by 120 volts which is 11.7 amps; and the lamp will draw 0.63 amps. Kirchhoff's junction rule says that the total current drawn through the circuit breaker that goes into this junction is going to equal the total current going out of the junction and we just figured out the three currents going out of the junction— the toaster current, the frying pan current and the lamp current— and so Kirchhoff's junction rule says that these three currents going out have to equal the current going in and this current going in is the current that will be through the fuse so that's 15 amps plus 11.7 amps plus 0.63 amps which is 27 amps. Now since that exceeds the 15 amp limit of this particular fuse, this combination will blow the 15 amp fuse.

