Question
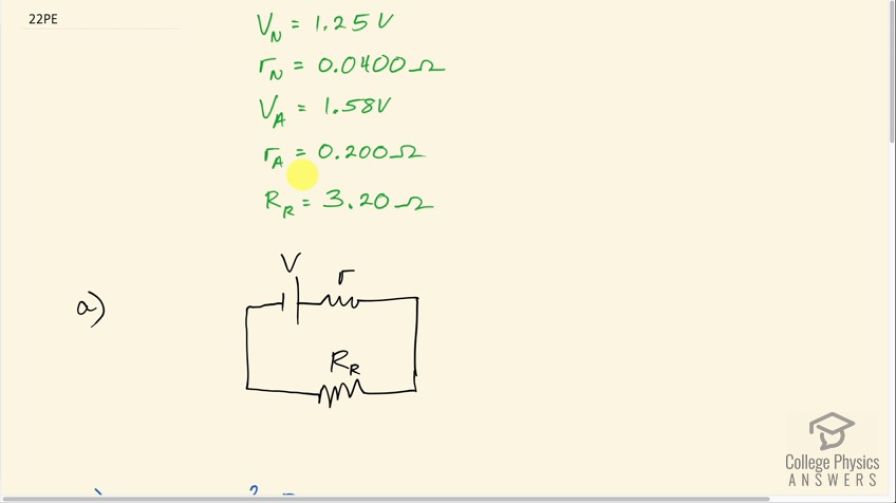
The label on a portable radio recommends the use of rechargeable nickel-cadmium cells (nicads), although they have a 1.25-V emf while alkaline cells have a 1.58-V emf. The radio has a resistance. (a) Draw a circuit diagram of the radio and its batteries. Now, calculate the power delivered to the radio. (b) When using Nicad cells each having an internal resistance of . (c) When using alkaline
cells each having an internal resistance of . (d)
Does this difference seem significant, considering that the radio’s effective resistance is lowered when its volume is turned up?
Final Answer
- Please see the solution video
- As the resistance decreases the power dissipated with either battery decreases as well, to the point where as the resistance approaches zero, the power dissipated in each case also approaches zero. This means the difference between the power dissipated in each case also approaches zero.
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 22 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In this question, we consider a radio with two different possibilities for the battery types. In one scenario, we'll have a nickel-cadmium battery with an emf of 1.25 volts and an internal resistance of 0.0400 ohms or there might be an alkaline battery, in which case, the emf is 1.58 volts and the internal resistance is 0.200 ohms. The resistance of the radio part of the circuit is 3.20 ohms and we have drawn the circuit in part (a) where we have the emf in series with its internal resistance and this combination is the battery and then all that is powering this radio circuit. So in part (b), we ask what is the power delivered to the radio using a nickel-cadmium cell? So the answer to that will be the current through this radio resistance multiplied by its resistance. Now in order to find the current though, we will have to find the emf divided by the total resistance of the whole circuit, which is the radio resistance plus the internal resistance of a battery and so I have written that here and all of this gets substituted in for I in this formula for power dissipated. So we have V over resistance of the radio plus the internal the resistance of the battery all squared multiplied by resistance of the radio. So in the case of a nickel-cadmium battery, we have V N over resistance of the radio plus the internal resistance of the nickel-cadmium battery all that squared times the radio resistance. So that's 1.25 volts divided by 3.20 plus 0.0400 ohms all squared times 3.20 ohms, which is 0.476 watts. In part (c), let's imagine there's an alkaline battery there in which case, we have 1.58 volts divided by 3.20 ohms plus 0.200 ohms— internal resistance for the alkaline battery— all squared times 3.20 ohms— radio circuit resistance— and that is 0.691 watts. In part (d), we are asked what if the volume is increased, which is done by reducing the resistance of the radio part of the circuit, how would the power difference compare with the power difference now? So right now the power difference with an alkaline battery versus a nickel-cadmium battery is 0.691 watts minus 0.476 watts, which is 0.215 watts. Well, as the resistance of the radio approaches zero, the power dissipated will both approach zero and we can see that by looking at this formula for... well, just look at this one here for the generic doesn't matter which type of battery we are talking about. As this radio resistance decreases, this product will decrease and on the other hand though, this denominator of this term or this factor I should say this denominator will increase... well, sorry the denominator decreases because the radio resistance is going down and by decreasing the denominator, we are increasing this quotient or this fraction but there's a limit to how small this denominator can get because it's being added to this internal resistance of the battery and so as the radio resistance goes down, eventually further reductions in the radio resistance won't matter because it will be just a tiny number added to this number here— the internal resistance—that's staying constant and so there's sort of a limit to how small this fraction can get. Meanwhile it's being multiplied by this factor which is continually decreasing and decreasing and so this power will eventually approach zero as the resistance approaches zero. So all that is to say then that the difference between the two will approach zero since we are comparing you know zero to zero. So at higher volumes, there will be no significant difference in the power dissipated with an alkaline versus a nickel-cadmium battery. (This is meant to be an N there).

