Question
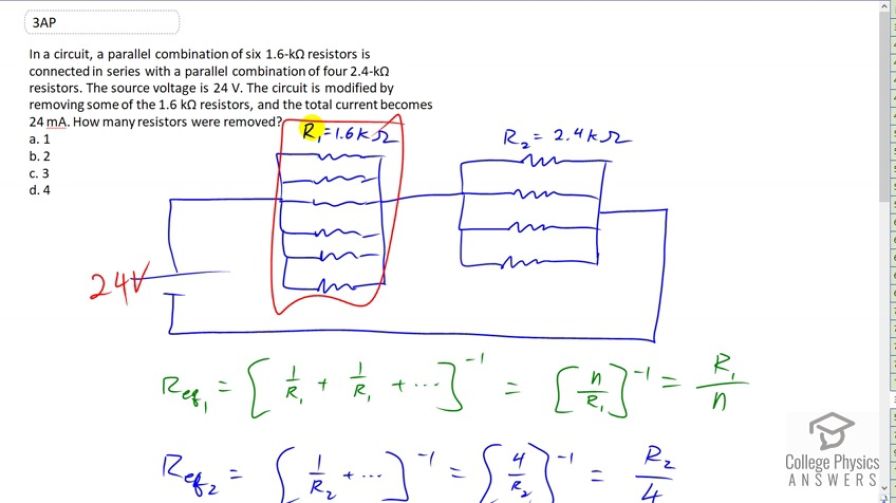
In a circuit, a parallel combination of six 1.6-kΩ resistors is connected in series with a parallel combination of four 2.4-kΩ resistors. The source voltage is 24 V. The circuit is modified by removing some of the 1.6 kΩ resistors, and the total current becomes 24 mA. How many resistors were removed?
- 1
- 2
- 3
- 4
Final Answer
(b)
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 3 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We have a circuit with a 24 Volt EMF and there are six resistors and each with the resistance of 1.6 kilo ohms in parallel. And we’re going to take some of these resistors away and after doing so, the current through the circuit will be 24 milli Amps. And the question will be how many resistors were taken away. So we’re going to calculate how many resistors there are. And go six minus that number to find the difference. And then this combination is connected in series with four resistors, each have resistance of 2.4 kilo ohms. So, we need to find the equivalent resistance of this whole circuit. And then we’ll say that the voltage, 24 Volts is current multiplied by that total resistance. So the equivalent resistance of these R1 resistors is going to be one over R1 plus another one over R1 plus another one over R1 and so on. However many times, we don’t really know. All to the power of negative one. And so there are going to be n resistors there and we have to solve for what that is in order to answer this question. So it’s n over R1 to the power of negative one which is the reciprocal of that so it’s R1 over n is the equivalent resistance of these resistors here. Then, likewise for these resistors, these 2.4 kilo ohms resistors, the equivalent resistance of those four in parallel will be four over R2 to the power of negative one which is R2 over four. Then, we say that the voltage is the current multiplied by the sum of those equivalent resistances because each of this collection of parallel resistors are in series. And so we just add them together. And substitute for each of them. And so we have R1 over n is the equivalent resistance one and then plus R2 over four. And then distribute the I into the brackets. And we have V equals IR1 over n plus Ir2 over four. And we want to isolate n. We’re going to begin by getting rid of this term. All of it to the left side. So we have V minus IR2 over four is IR1 over n. And then we’ll multiply both sides by n over V minus IR2 over four. So it cancels in the left, leaving us with the n in the left. On the right side, we have IR1 over V minus IR2 over four. It says 24 times ten to the minus three Amps times 1.6 to the ten times 3 ohms divided by 24 Volts minus 24 times ten to the minus three Amps times 2.4 times ten to the positive three ohms over four. And we end up with four. And that’s the number of resistors that there are here. And so the number taken away is six minus four which is two. And so the answer to this question is b.


