Question
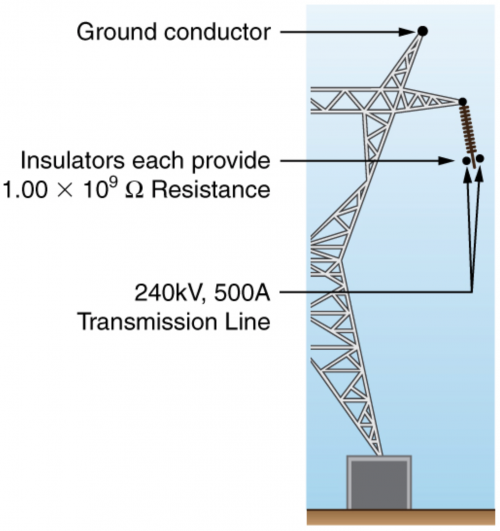
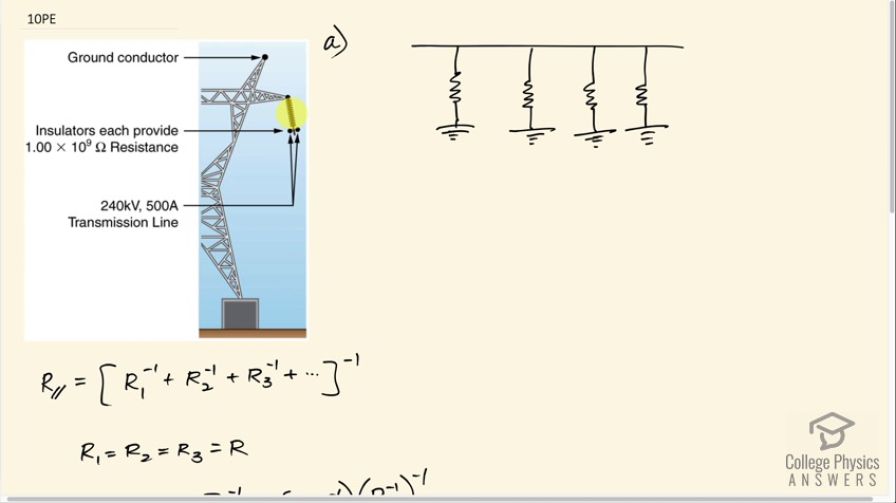
A 240-kV power transmission line carrying is hung from grounded metal towers by ceramic insulators, each having a resistance. Figure 21.51. (a) What is the resistance to ground of 100 of these insulators? (b) Calculate the power dissipated by 100 of them. (c) What fraction of the power carried by the line is this? Explicitly show how you follow the steps in the Problem-Solving Strategies for Series and Parallel Resistors.
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 10 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
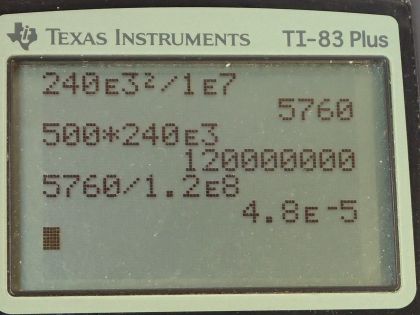
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. Consider a high voltage power line at 240 kilovolts and as it's traveling along, it's connected to these towers by a ceramic insulator and each of these insulators has a resistance of 1.00 times 10 to the 9 ohms and we can imagine that these insulators, one after another, are all resistors connected in parallel with this power line being this line here and each of these other ends of this ceramic insulator is connected to ground and so this insulator is preventing all the current from the high voltage line going to ground. So these are all connected to ground, which means essentially that they are connected together, and because ground will have the same potential in, you know, each location... we can assume... especially if there are one hundred consecutive insulators. And so we can think of this as being like this circuit— I'll draw it in a way that might be more familiar— where each of these resistors here are the insulators and this end of this terminal of this, you know, imaginary battery is the ground and this end is the high potential power line. Okay! So we want to find the equivalent resistance then of one hundred of these... so ... one hundred of these ceramic insulators or resistors, whichever you wanna call them. So the equivalent resistance then will be the reciprocal of the sum of the reciprocal of each of these resistances. Often this formula is written with fractions and we can do that so 1 over R parallel equals 1 over R 1 plus 1 over R 2 plus so on and so on and that would be fine and then to solve for R parallel, you would have to raise both sides to exponent negative 1 in order to flip the left side and then the right hand side, you can't flip sums because these are separate terms, you can't just flip the whole thing so you have to write bracket exponent negative 1 and so you might see R parallel equals 1 over R 1 plus 1 over R 2 plus so on all to the power of negative 1 and that's the same thing that I have written here but I have just written it in a way that looks a little different because I like to plug things into my calculator using my exponent negative 1 button. So I will put in one resistance and click the button for negative 1 exponent plus the next resistance negative 1 exponent and so on and then take that sum and click that negative 1 exponent button again to get the answer. Okay! All these resistances are the same— they are all the same ceramic insulators— and so we have 100 of them and so we are going to be multiplying by a hundred because that's what multiply means, you know, add something together this many times. So we have 100 times one of the resistances to the exponent negative 1 and we can raise both factors in here to the exponent negative 1 so we have a 100 to the negative 1 and then R to the negative 1 to the negative 1 which makes it R and then 100 to the negative 1 makes it 1 over a 100 and we end up with R over 100. So the equivalent resistance then is 1.00 times 10 to the 9 ohms divided by 100, which is 1.00 times 10 to the 7 ohms. Part (b) asks what power is dissipated by all these ceramic insulators? Well, it will be the potential difference across them squared divided by their resistance So that's 240 times 10 to the 3 volts is the difference between the power line and the ground so that's the potential difference across each of the ceramic insulator and we square that and divide by 1.00 times 10 to the 7 ohms— total equivalent resistance— and that's 5760 watts and that might seem like a big number but we have to compare it in part (c) to the total power delivered by the lines, which will be the product of the current and the voltage. So that's 500 amps we are told here multiplied by 240 kilovolts and that's 1.20 times 10 to the 8 watts and so we take this fraction that's lost in the resistors by dividing that by the total power delivered which is 4.80 times 10 to the minus 5. So this power loss is a small fraction of the total power that's carried by the lines.