Question
Electric fish generate current with biological cells called electroplaques, which are physiological emf devices. The electroplaques in the South American eel are arranged in 140 rows, each row stretching horizontally along the body and each containing 5000 electroplaques. Each electroplaque has an emf of 0.15 V and internal resistance of . If the water surrounding the fish has resistance of , how much current can the eel produce in water from near its head
to near its tail?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 27 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
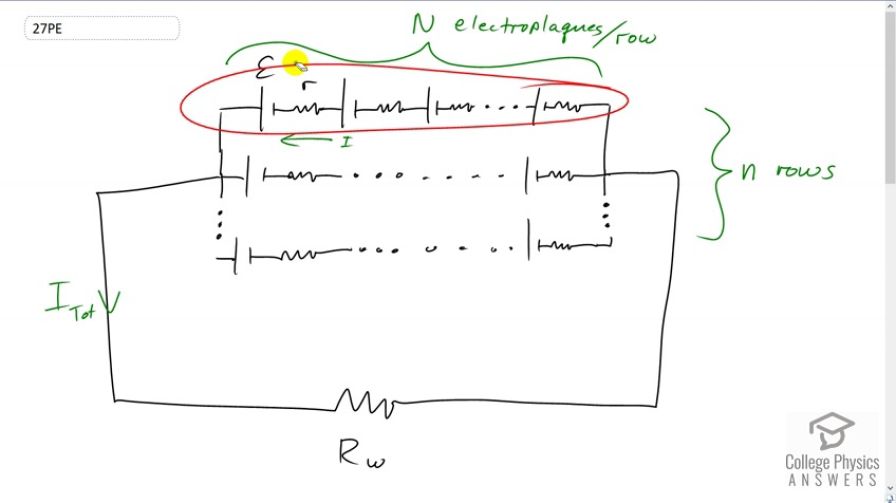
This is College Physics Answers with Shaun Dychko. So the side of the body of the electric eel consists of rows of electroplaques. This is one electroplaque here and there are five thousand of them in one row. There are 140 rows of them and so this is the schematic. So an electroplaque consists of an EMF that we're given and an internal resistance as well. So we have a whole bunch of EMFs and internal resistances connected in series along one row. Then we have 140 rows like that in parallel. All of this is connected to the water and there is 800 ohms resistance in the water. Our job is to figure out what is this total current that comes between the head and the tail of the eel. So this is where the head would be and that would be the tail, say. So we can use the junction rule at this point to say that the total current coming out of the junction, I subscript tot for total, is equal to the number of rows multiplied by the current I through each row. So I've written that here and then to solve for this I total we need to have another equation because we don't know what the current is through the single row. So our second equation we'll get from the loop rule which is here. What I've done is said that starting from here say, we go across one row, we traverse one row in this direction in which case we have a positive potential difference here since we're going from the negative to the positive terminal of each of these EMFs. The total voltage across this entire row will be the number of electroplaques multiplied by the terminal voltage of one electroplaque. That is the terminal voltage so we have the EMF of an electroplaque minus the current through the electroplaque multiplied by its internal resistance. We have N of those in a row, capital N. Then as we continue our loop traversal, we go through the resistance of the water in the direction of the current and so that's going to be minus I subscript total multiplied by the resistance of the water. All this equals zero. So from this equation we can do a little bit of algebra and say that I is I total divided by small n which is the number of rows. This is useful because we want to have an equation consisting only of the variable I total. So we replace the variable I which we don't actually care about with this I total divided by n. Now this equation here is good because we know everything in it except for I total. So now we do some algebra to solve for that. So we take both of these terms to the right hand side and then switch the sides around so that I am adding those terms to both sides. We end up with I total times capital N over small n times internal resistance r, plus I total times resistance of the water, equals the number of electroplaques in a single row multiplied by the EMF per electroplaque. Then factor out the I total to get this line here and then divide by this binomial both sides, and end up with the total current is number of electroplaques in a row multiplied by the EMF per electroplaque, divided by number of electroplaques in a row, divided by the number of rows times the internal resistance per electroplaque plus the resistance of the water. So this is five thousand times 0.15 volts, divided by five thousand over 140 times 0.25 ohms, plus 800 ohms, gives us 0.93 amps as the total current coming between the head and tail of the eel.
