Question
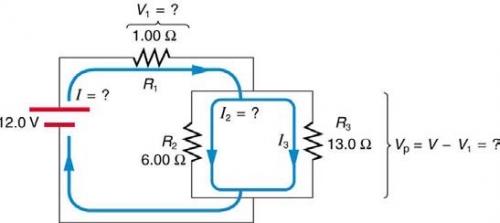
Referring to the example combining series and parallel
circuits and Figure 21.6, calculate in the following two
different ways: (a) from the known values of and ; (b)
using Ohm’s law for . In both parts explicitly show how
you follow the steps in the Problem-Solving Strategies for Series and Parallel Resistors.
From the example: , and .
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 7 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
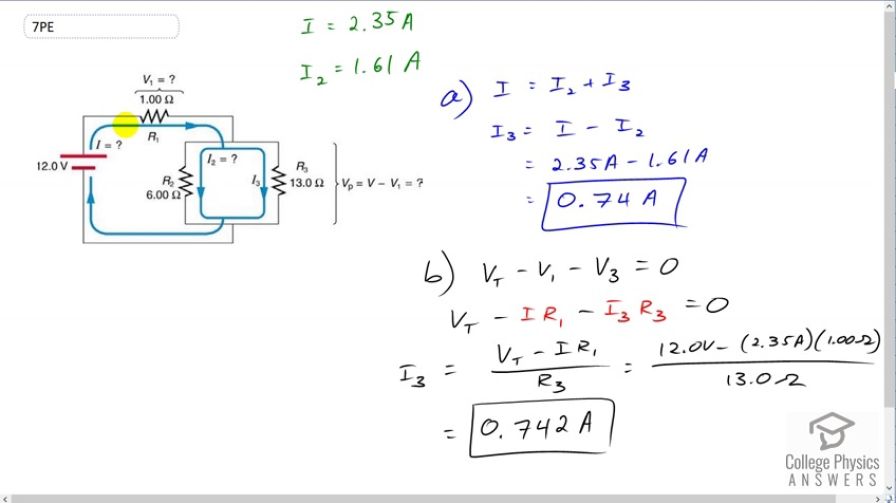
This is College Physics Answers with Shaun Dychko. So in the circuit we have a 12 volt EMF source and there is a current I going clockwise. It goes to this resistor number one, which has a resistance of one ohm, and then passes through this parallel branch of two resistors. The resistance R three is 13 ohms and we want to find out what is the current going through that resistor. So we're given that I is 2.35 amps and I two, the current through the R two resistor is 1.61 amps. We can use the junction rule which is to say that all the current going into this junction has to equal the total current coming out of the junction. So the total current going in is I and the total current coming out is I two plus I three. That's what we've written on this side. So we solve this for I three by subtracting I two from both sides and then switching the sides around. So I three is I minus I two which is 2.35 amps minus 1.61 amps which is 0.74 amps. Then in part B, we're asked to solve the same question, what is I three by using a method involving Ohm's Law. Ohm's Law is V equals IR. So we have the Loop Rule is going to help us here. So let's consider a loop where we begin here and traverse in this direction in which case we have a positive potential difference from the starting point to here across this EMF. So that's V t our terminal voltage I called it there, and then we're going in the same direction as the current across this resistor and so this is a drop in potential. So that's negative V one. Then we're going to go along this branch across R three again in the direction of the current. So we're going to have a negative potential difference there and that's minus V three and then we're done our loop. Then we substitute I R in place of each of these voltagesV one and V three. So V one is going to be the current I multiplied by resistance one. Then V three is going to be the current I three multiplied by resistance three. Then we solve this for I three and we move this to the right hand side making it positive and then divide both sides by R three and we solve for I three. So I three is V t minus I times R one over R three. That is 12 volts minus 2.35 amps times one ohm, divided by 13 ohms, giving us 0.742 amps which is to two significant figures, the same as the answer in part A.
