Question
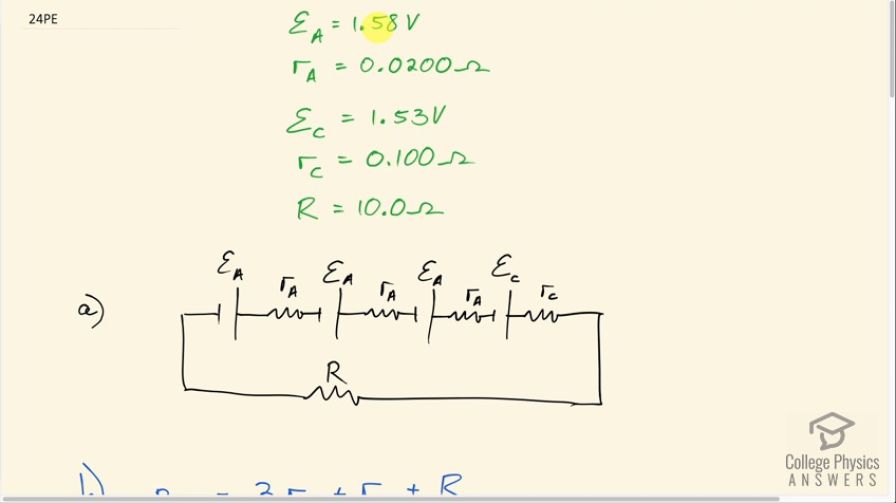
A child’s electronic toy is supplied by three 1.58-V alkaline cells having internal resistances of in series with
a 1.53-V carbon-zinc dry cell having a internal resistance. The load resistance is . (a) Draw a
circuit diagram of the toy and its batteries. (b) What current flows? (c) How much power is supplied to the load? (d) What is the internal resistance of the dry cell if it goes bad, resulting in only 0.500 W being supplied to the load?
Final Answer
- Please see the solution video
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 24 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A toy is powered by three alkaline batteries, each with an emf of 1.58 volts and internal resistance of 0.0200 ohms and one carbon-zinc battery, which has an emf of 1.53 volts and an internal resistance of 0.100 ohms and the resistance of the toy or the load in other words is 10.0 ohms and here's a circuit diagram of that where we have one, two, three alkaline batteries and one carbon-zinc battery all in series with the load resistance. In part (b), we are asked to find what current flows? So we need to find the equivalent resistance of all one, two, three, four, five resistors here, three of which are the internal resistance of the alkaline battery plus the carbon-zinc internal resistance plus the load resistance. And we need to know what the total emf is which is three times the emf of an alkaline battery plus the emf of the carbon-zinc battery and the current will be this total emf divided by the total equivalent resistance. So that's 3 ε A plus ε C divided by 3r A plus r C plus R. So that's 3 times 1.58 volts plus 1.53 volts all divided by 3 times 0.0200 ohms— this is the internal resistance of an alkaline battery— plus 0.100 ohms—the internal resistance of the carbon-zinc battery— plus 10.0 ohms—resistance of the toy— and that is 0.617 amps. The total power dissipated in the load or the resistor which is the toy, is the current flowing through it squared multiplied by the resistance of the toy. So that's 0.617 amps squared multiplied by 10.0 ohms which is 3.81 watts. In part (d), we are told that the power being dissipated in the load is now 0.500 watts. So given that we know that and we know that that internal resistance of the dry cell has increased and that's responsible for this reduced current which is causing a reduced power dissipation, what must be the internal resistance of the carbon-zinc battery be? We can rearrange this to solve for this new current— I am calling it current prime to distinguish it from the current that we had before in parts (b) and (c)— and the current prime squared, after we divide both sides by the resistance of the toy, is this new power dissipated in the resistor, which we call P R prime, divided by the resistance of the toy which does not need a prime because it hasn't changed and we take the square root of both sides to solve for the current prime. And then we also can make an expression for the current prime in terms of the resistance of the carbon-zinc internal resistance. So we could turn this into a number at this point by the way but I am just gonna substitute with letters into this expression that we are going to develop here in blue. So our job with this formula, which we came up with in part (b) here, I just copied the same formula but now it's a new resistance for this carbon zinc-battery which means it should probably have a prime on it I guess if we are gonna have primes to distinguish this new scenario. Before the resistance was 0.100 ohms but now it's something bigger and we'll multiply both sides by this denominator in which case, we have I prime times 3r A plus r C prime plus R all equals 3ε A plus ε C and then distribute the I prime into this bracket here multiplying each term by I prime and we end up with this line here and then take away the two terms that do not contain r c prime from the left by subtracting them away so minus RI prime from both sides and then minus 3r AI prime from both sides and then we have r C primeI prime equals 3ε A plus ε C minus 3r AI prime minus RI prime and then divide both sides by this current. And then we have solved for the internal resistance of the carbon-zinc battery and then we'll divide this I prime into the two terms that contain I prime so that they just become minus 3r A minus R and then leave it underneath this part here. You don't have to do that... that's just a personal preference thing... we could plug in square root P R prime over R in three different places if we wanted to but by doing this step here, we have only one place to make that substitution for the current I prime. So here we are substituting this expression in place of I prime and then we can plug in numbers. So we have three times the emf of the alkaline battery— 1.58 volts— plus the emf of the carbon-zinc battery— 1.53 volts— divided by the square root of the new power dissipated in the load, which is 0.500 watts divided by the resistance of the load, which is 10.0 ohms, minus 3 times the internal resistance of the alkaline battery of 0.0200 ohms minus 10.0 ohms of the load and that works out to 18.0 ohms must be the resistance internally internally of the carbon-zinc battery now.

