Question
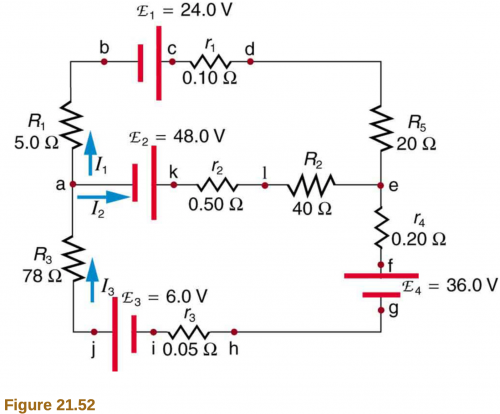
Apply the loop rule to loop abcdefghija in Figure 21.52.
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics for AP® Courses, Chapter 21, Problem 36 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. In figure [21.52], we are meant to apply the Loop rule to the loop beginning at the point a and then going to point b and then c and d and e and then from here continue down to f, g, h, i, j and then back to a and we are traversing the loop in this direction— we are always going up on the left, down on the right and to the left on the bottom and to the right on the top. Okay! So starting at point a, we are traversing upwards through this resistor in the same direction as the current I 1 through it and so that means there's a potential drop here or in other words, a negative change in potential so we have negative I 1 times R 1 is the term for this particular resistor. And then we start from the negative terminal of this emf and end at the positive terminal so that's an increase in potential so we have positive emf one. And then we are traversing resistor little r 1 in the same direction as the current through it because I 1 is going to the right here as well and I 1 is going down here and so this is a drop in potential here when traversing a resistor in the same direction as the current through it so that's minus I 1 times r 1 and then minus I 1 times R 5 and then minus I 3 because that's the current in this section from point e and down through the bottom part— this is all current I 3— and so we have minus I 3 times r 4 is the potential drop here because we are traversing downwards in the same direction as the current I 3 here I 3 is going up on the left, which means it's going to the left in the bottom branch and that means it's going down in the right hand branch. Okay! And then traversing this emf, we are beginning at the positive terminal and ending at the negative terminal so that's a potential drop and so we have a minus emf four there and then we traverse to the left through this resistor in the same direction as the current through it so that's minus I 3r 3 and then going from the negative terminal ending at the positive terminal of this battery is an increase in potential then because we end at the higher potential... you know, think of the longer line as being a higher length and therefore higher potential so we have plus emf three and then we have minus I 3 times R 3 and once we return to our starting point, we know that this entire loop has to have a total change in potential of zero because energy needs to be conserved and so we put equals zero here.